Contents

Distâncias e matrizes

A matriz de distância é feita através da utilização da função pdist; como já mencionado a distância euclidiana entre dois pontos \(p\) e \(q\) é \( d\left( p,q\right) = \sqrt {\sum _{i=1}^{n} \left( q_{i}-p_{i}\right)^2 }\), para \(n\) dimensões. De forma a facilitar a intuição de como esta distância é aplicada ao registo de votações vamos, passo a passo, analisar um caso simplificado (o que nos serve também de forma de validação indirecta do processo).

Vamos criar um cenário com três partidos, com nomes que reflectem o seu perfil de votação:

  • O Partido Favorável vota a favor.

  • O Partido Abstencionista abstem-se (pelo menos até certo ponto).

  • O Partido do Contra vota contra.

Uma votação, \( n = 1 \)

Começemos por uma única votação, onde cada um dos partidos segue a sua linha programática:

v1=[[1],[0],[-1]]
v1_df = pd.DataFrame(v1, columns=["v1"], index=["F","A", "C"])
v1_df
v1
F 1
A 0
C -1

Com uma única votação o número de dimensões é de \(n = 1\) e é bastante intuitivo que a distância entre eles é a norma:\( d\left( x,y\right) = | x - y |\); entre 1 e 0 a distância é 1, entre 1 e -1 a distância é 2, etc. Para \( n = 1 \) a distância euclidiana é equivalente à norma, pois \( \sqrt{\left( q - p\right)^2} = | q - p | \), como pode ser observado quando medidas a distância entre eles:

import math
## We could also sue the array directly, e.g.
## print("Distance from" , a[0][0] , "and" , a[1][0],"=",math.sqrt((a[0][0]-a[1][0]) ** 2))

print("Distance from", v1_df.loc["F"].name, "and", v1_df.loc["A"].name, "=", 
      math.sqrt((v1_df.loc["F"]["v1"]-v1_df.loc["A"]["v1"]) ** 2))
print("Distance from", v1_df.loc["F"].name, "and", v1_df.loc["C"].name, "=", 
      math.sqrt((v1_df.loc["F"]["v1"]-v1_df.loc["C"]["v1"]) ** 2))
print("Distance from", v1_df.loc["A"].name, "and", v1_df.loc["C"].name, "=", 
      math.sqrt((v1_df.loc["A"]["v1"]-v1_df.loc["C"]["v1"]) ** 2))

Distance from F and A = 1.0
Distance from F and C = 2.0
Distance from A and C = 1.0

Temos a distância entre os três possíveis pares: a distância entre F e A é idêntica à distância entre A e F. Isto é importante porque ajuda a explicar a diferença entre a forma “condensada” e forma “quadrada”. A função pdist retorna a distância entre os vários pares na forma condensada:

pdist(v1_df)

array([1., 2., 1.])

Estes são os mesmos valores que obtivemos de forma manual, e é isso que a função faz: calcula uma determinada distância (euclidiana, neste caso e por omissão) entre todos os pares possíveis, sem que seja necessário especificarmos todas as combinações possíveis.

Este formato condensado não é o que permite uma leitura mais imediata, e para tal existe a função squareform que apresenta os mesmos resultados mas numa matriz simétrica:

squareform(pdist(v1_df))

array([[0., 1., 2.],
       [1., 0., 1.],
       [2., 1., 0.]])

Em formato tabular torna-se ainda mais claro… e isto é exactmante a matriz de distância usada para o mapa térmico

v1_distmat=pd.DataFrame(squareform(pdist(v1)), columns=v1_df.index, index=v1_df.index)
v1_distmat
F A C
F 0.0 1.0 2.0
A 1.0 0.0 1.0
C 2.0 1.0 0.0

Geometricamente temos pontos numa recta: uma análise das distâncias entre os três partidos com base no histórico de votação seria simples de visualizar com base na posição desses pontos:

fig, ax = plt.subplots()
ax.axhline(y=0,c="gold",zorder=-1)

for x in v1_df["v1"]:
    ax.scatter(x,y=0,)
plt.show()
_images/met_distmat_12_0.png

Com base na matriz de distância contruimos o mapa térmico de forma muito simples:

plt.figure(figsize=(4,4))
sns.heatmap(
    v1_distmat,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    annot = True,
    square =True,
)
plt.show()
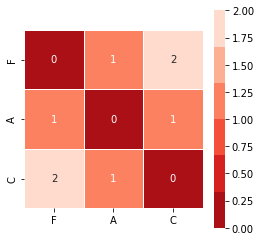
_images/met_distmat_14_0.png

…e o agrupamento com base nessa matriz:

v1_distmat_link = hc.linkage(pdist(v1_df))

sns.clustermap(
    v1_distmat,
    annot = True,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    row_linkage=v1_distmat_link,
    col_linkage=v1_distmat_link,
    figsize=(4,4)
)
plt.show()
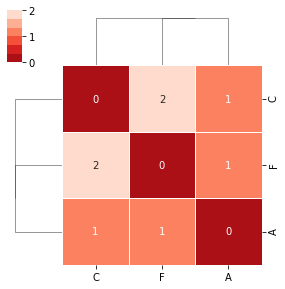
_images/met_distmat_16_0.png

Duas votações, \( n = 2 \)

Usando a mesma abordagem (agora sem necessidade de explicações adicionais) adicionamos mais uma votação, sempre em linha com o perfil fixo de votos de cada um: cada partido passa a ter dois votos, logo temos duas dimensões:

v2=[[1,1],[0,0],[-1,-1]]
v2_df = pd.DataFrame(v2, columns=["v1","v2"], index=["F","A", "C"])
v2_df
v1 v2
F 1 1
A 0 0
C -1 -1

A distância euclidiana é agora feita de forma mais genérica: a raíz quadrada da soma do quadrado das diferenças: para a primeira diferença isto significa, passo a passo e para \(q=F\) e \(p=A\):

\( d\left(q,p\right) = \sqrt {\sum _{i=1}^{n} \left( q_{i}-p_{i}\right)^2 } = \sqrt{\left( q_{1}-p_{1}\right)^2 + \left( q_{2}-p_{2}\right)^2 } = \sqrt{\left( 1 - 0\right)^2 + \left( 1 - 0\right)^2} = \sqrt{ 1^2 + 1^2 } = \sqrt{1+1} = \sqrt{2} \approx 1.4142135623730951 \)

E de facto:

print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v2_df.loc["F"],v2_df.loc["A"]))))
print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v2_df.loc["F"],v2_df.loc["C"]))))
print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v2_df.loc["A"],v2_df.loc["C"]))))

1.4142135623730951
2.8284271247461903
1.4142135623730951

Tal como antes é idêntico ao resultado de pdist, tanto na sua forma condensada como quadrada:

print("pdist:\n", pdist(v2),"\n")
print("squareform:\n",squareform(pdist(v2)))
v2_distmat=pd.DataFrame(squareform(pdist(v2)), columns=v2_df.index, index=v2_df.index)
v2_distmat

pdist:
 [1.41421356 2.82842712 1.41421356] 

squareform:
 [[0.         1.41421356 2.82842712]
 [1.41421356 0.         1.41421356]
 [2.82842712 1.41421356 0.        ]]
F A C
F 0.000000 1.414214 2.828427
A 1.414214 0.000000 1.414214
C 2.828427 1.414214 0.000000

Com duas votações temos \( n = 2 \) e conseguimos ver os pontos num espaço cartesiano em \( \mathbb{R}^2 \) (um plano).

fig, ax = plt.subplots()
for x,y in zip(v2_df["v1"], v2_df["v2"]):
    ax.scatter(x,y)
_images/met_distmat_24_0.png

A matriz de distância seria neste caso, como no anterior, desnecessária (em \( \mathbb{R}^2 \) as distâncias entre os partidos são óbvias por facilmente visualizáveis); a forma de a construir é idêntica:

plt.figure(figsize=(4,4))

sns.heatmap(
    v2_distmat,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    annot = True,
    square =True,
)
plt.show()
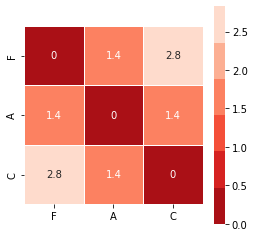
_images/met_distmat_26_0.png

… e o clustermap que agrega distâncias e agrupamento num único gráfico:

v2_distmat_link = hc.linkage(pdist(v2_df))

sns.clustermap(
    v2_distmat,
    annot = True,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    row_linkage=v2_distmat_link,
    col_linkage=v2_distmat_link,
    figsize=(4,4)
)
plt.show()
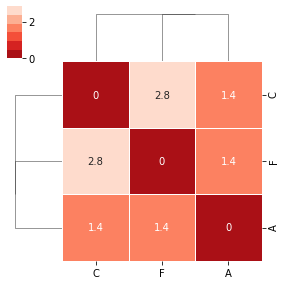
_images/met_distmat_28_0.png

Três votações, \( n = 3 \)

Este é o último caso onde a visualização pode ser feita de forma directa. Consideremos:

v3=[[1,1,1],[0,0,0],[-1,-1,-1]]
v3_df = pd.DataFrame(v3, columns=["v1","v2", "v3"], index=["F","A", "C"])
v3_df
v1 v2 v3
F 1 1 1
A 0 0 0
C -1 -1 -1

A distância é calculada da mesma forma:

print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v3_df.loc["F"],v3_df.loc["A"]))))
print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v3_df.loc["F"],v3_df.loc["C"]))))
print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v3_df.loc["A"],v3_df.loc["C"]))))

1.7320508075688772
3.4641016151377544
1.7320508075688772

… bem como a matriz de distância:

print("pdist:\n", pdist(v3),"\n")
print("squareform:\n",squareform(pdist(v3)))
v3_distmat=pd.DataFrame(squareform(pdist(v3)), columns=v3_df.index, index=v3_df.index)
v3_distmat

pdist:
 [1.73205081 3.46410162 1.73205081] 

squareform:
 [[0.         1.73205081 3.46410162]
 [1.73205081 0.         1.73205081]
 [3.46410162 1.73205081 0.        ]]
F A C
F 0.000000 1.732051 3.464102
A 1.732051 0.000000 1.732051
C 3.464102 1.732051 0.000000

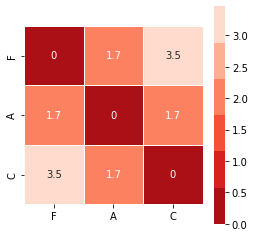
e o correspondente mapa térmico:

plt.figure(figsize=(4,4))

sns.heatmap(
    v3_distmat,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    annot = True,
    square =True,
)
plt.show()
_images/met_distmat_36_0.png

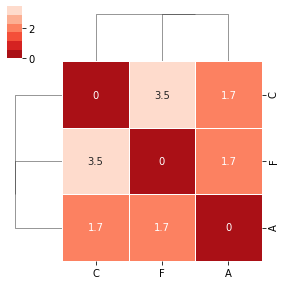
O clustermap apresenta os mesmos valores, mas reordenando colunas e linhas de forma a apresentar o resultado do agrupamento; note-se que, neste caso, não é apresentado nenhum agrupamento entre 2 dos partidos pois todos divergem de forma equidistante, constituindo três grupos separados:

v3_distmat_link = hc.linkage(pdist(v3_df))

sns.clustermap(
    v3_distmat,
    annot = True,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    row_linkage=v3_distmat_link,
    col_linkage=v3_distmat_link,
    figsize=(4,4)
)
plt.show()
_images/met_distmat_38_0.png

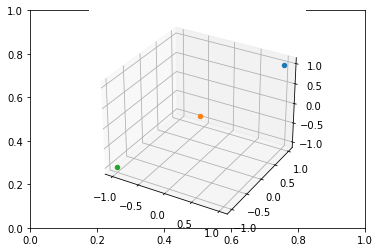
Estamos agora em \( \mathbb{R}^3 \), e para visualizar podemos usar uma projecção tridimensional:

fig, ax = plt.subplots()
ax = fig.add_subplot(111,projection='3d')

for x,y,z in zip(v3_df["v1"], v3_df["v2"], v3_df["v3"]):
    ax.scatter(x,y,z)
_images/met_distmat_40_0.png

Mais de três votações, \( n > 3 \)

A partir daqui coloca-se a questão fundamental: a impossibilidade de visualizar de forma directa a distância para além das três dimensões. A distância existe e segue exactamente os mesmo passos, simplesmente não é passível de visualização, razão pela qual é necessário (agora sim) depender de formas que “reduzam” as dimensões e as tornem visualizáveis.

Até agora os agrupamentos têm sido sempre iguais pois a distância é sempre linear; vamos neste último caso assumir que o Partido Abstencionista teve uma mudança de posição e passou a votar por vezes a favor e contra, embora mais contra que a favor:

v4=[[1,1,1,1,1,1,1,1,1,1],[0,0,0,1,0,-1,0,-1,-1,-1],[-1,-1,-1,-1,-1,-1,-1,-1,-1,-1]]
v4_df = pd.DataFrame(v4, columns=["v1","v2", "v3","v4","v5","v6","v7","v8","v9","v10"], index=["F","A", "C"])
v4_df
v1 v2 v3 v4 v5 v6 v7 v8 v9 v10
F 1 1 1 1 1 1 1 1 1 1
A 0 0 0 1 0 -1 0 -1 -1 -1
C -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

A distância calculdada “manualmente”:

print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v4_df.loc["F"],v4_df.loc["A"]))))
print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v4_df.loc["F"],v4_df.loc["C"]))))
print(math.sqrt(sum((px - qx) ** 2.0 for px, qx in zip(v4_df.loc["A"],v4_df.loc["C"]))))

4.58257569495584
6.324555320336759
3.0

… e o cálculo via pdist e a matriz de distância:

print("pdist:\n", pdist(v4),"\n")
print("squareform:\n",squareform(pdist(v4)))
v4_distmat=pd.DataFrame(squareform(pdist(v4)), columns=v4_df.index, index=v4_df.index)
v4_distmat

pdist:
 [4.58257569 6.32455532 3.        ] 

squareform:
 [[0.         4.58257569 6.32455532]
 [4.58257569 0.         3.        ]
 [6.32455532 3.         0.        ]]
F A C
F 0.000000 4.582576 6.324555
A 4.582576 0.000000 3.000000
C 6.324555 3.000000 0.000000

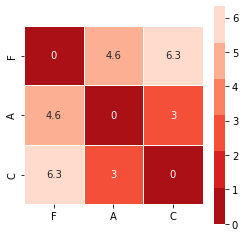
O mapa térmico:

plt.figure(figsize=(4,4))

sns.heatmap(
    v4_distmat,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    annot = True,
    square =True,
)
plt.show()
_images/met_distmat_49_0.png

… e o dendograma, já apresentando um agrupamento com base na maior aproximação com base no registo de votação:

v4_distmat_link = hc.linkage(pdist(v4_df), method="ward")

sns.clustermap(
    v4_distmat,
    annot = True,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    row_linkage=v4_distmat_link,
    col_linkage=v4_distmat_link,
    figsize=(4,4)
)
plt.show()
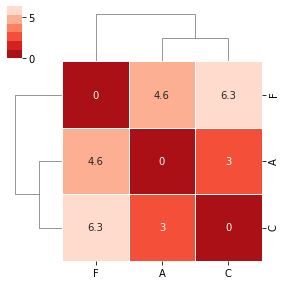
_images/met_distmat_51_0.png

E aqui pode ser observado o resultado (e a utilidade) do cálculo das distâncias e da utilização de clustering: ao observarmos os votos acima conseguimos, intuitivamente, determinar que o partido do A está mais próximo do C, mas fazer o mesmo para 100, 1000 ou 10000 votações seria manifestamente mais difícil.