3. A XIII Legislatura: o princípio¶
Da Rosa, nada digamos por agora.
—Sampaio Bruno, «Os Cavaleiros do Amor»
3.1. As eleições legislativas de 2015¶
A XIII Legislatura resultou das eleições legislativas de 2015. Os resultados colocam a coligação «Portugal à Frente» (PSD e CDS-PP) à frente com 39% dos votos. O processo de formação do governo iria, contudo, introduzir uma novidade no histórico político nacional: a formação de Governo pela segunda força mais votada (PS) suportado para tal por uma maioria de Esquerda (BE, PCP e PEV).
3.2. Os dados das votações¶
Total de votações: 6393
Data limite inferior: 2015-10-23
Data limite superior: 2019-10-24
Para a XIII legislatura os dados analisados dizem exclusivamente respeito às Iniciativas parlamentares (as Actividades, em menor número e que dizem respeito a temas como votos de pesar ou condenação, não estão presentes na página do Parlamento de Dados Abertos).
O processamento inicial resulta num conjunto bastante alargado de colunas e observações (votações, uma por linha), nomeadamente os votos dos vários partidos:
with pd.option_context("display.max_columns", 0):
display(votes[["resultado"] + parties])
| resultado | BE | PCP | PEV | PS | PAN | PSD | CDS-PP | |
|---|---|---|---|---|---|---|---|---|
| 0 | Aprovado | A Favor | A Favor | A Favor | A Favor | A Favor | Abstenção | A Favor |
| 1 | Aprovado | A Favor | A Favor | NaN | A Favor | NaN | A Favor | A Favor |
| 2 | Aprovado | A Favor | A Favor | A Favor | A Favor | A Favor | Abstenção | A Favor |
| 3 | Aprovado | A Favor | A Favor | NaN | A Favor | NaN | A Favor | A Favor |
| 4 | Aprovado | A Favor | A Favor | A Favor | A Favor | A Favor | Abstenção | Abstenção |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 6395 | Aprovado | Abstenção | Abstenção | Abstenção | A Favor | A Favor | A Favor | A Favor |
| 6396 | Aprovado | Abstenção | Abstenção | Abstenção | A Favor | A Favor | A Favor | A Favor |
| 6397 | Aprovado | A Favor | A Favor | A Favor | A Favor | A Favor | A Favor | A Favor |
| 6398 | Aprovado | A Favor | A Favor | A Favor | A Favor | A Favor | A Favor | A Favor |
| 6399 | Aprovado | A Favor | A Favor | A Favor | A Favor | A Favor | A Favor | A Favor |
6393 rows × 8 columns
3.3. Mapa térmico das votações¶
O mapa térmico de votações para a legislatura – recordemos que nos permite ver através de cores todas as votações, dando uma imagem geral do comportamento dos vários partidos – é o seguinte:
votes_hmn = votes_hm.replace(["A Favor", "Contra", "Abstenção", "Ausência"], [1,-1,0,-2]).fillna(0)
##RYG
voting_palette = ["black","#FB6962","#FCFC99","#79DE79",]
fig = plt.figure(figsize=(8,8))
sns.heatmap(votes_hmn ,
square=False,
yticklabels = False,
cbar=False,
cmap=sns.color_palette(voting_palette),
linewidths=0,
)
plt.show()
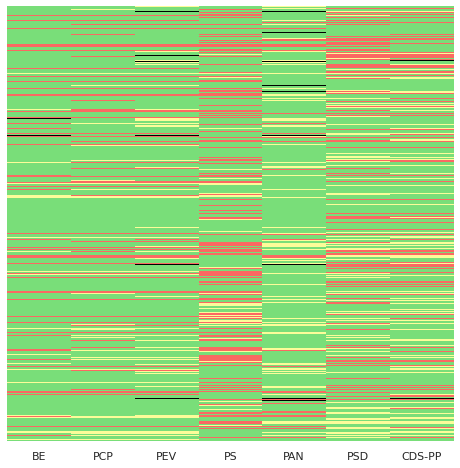
3.4. Votações idênticas¶
Das votações da legislatura é esta a matriz de votações idênticas:
pv_list = []
def highlight_diag(df):
a = np.full(df.shape, '', dtype='<U24')
np.fill_diagonal(a, 'font-weight: bold;')
return pd.DataFrame(a, index=df.index, columns=df.columns)
## Not necessarily the most straightforard way (check .crosstab or .pivot_table, possibly with pandas.melt and/or groupby)
## but follows the same approach as before in using a list of dicts
for party in votes_hm.columns:
pv_dict = collections.OrderedDict()
for column in votes_hmn:
pv_dict[column]=votes_hmn[votes_hmn[party] == votes_hmn[column]].shape[0]
pv_list.append(pv_dict)
pv = pd.DataFrame(pv_list,index=votes_hm.columns)
pv.style.apply(highlight_diag, axis=None)
| BE | PCP | PEV | PS | PAN | PSD | CDS-PP | |
|---|---|---|---|---|---|---|---|
| BE | 6393 | 5659 | 5554 | 4179 | 4641 | 3225 | 3356 |
| PCP | 5659 | 6393 | 5837 | 4162 | 4360 | 3265 | 3354 |
| PEV | 5554 | 5837 | 6393 | 3866 | 4802 | 2989 | 3065 |
| PS | 4179 | 4162 | 3866 | 6393 | 3642 | 3641 | 3525 |
| PAN | 4641 | 4360 | 4802 | 3642 | 6393 | 3308 | 3426 |
| PSD | 3225 | 3265 | 2989 | 3641 | 3308 | 6393 | 5301 |
| CDS-PP | 3356 | 3354 | 3065 | 3525 | 3426 | 5301 | 6393 |
A visualização desta matriz através de um mapa térmico:
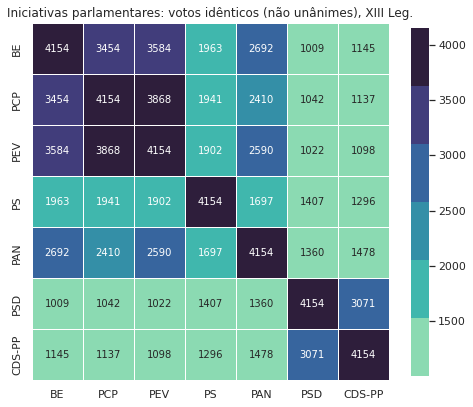
| BE | PCP | PEV | PS | PAN | PSD | CDS-PP | |
|---|---|---|---|---|---|---|---|
| BE | 4154 | 3454 | 3584 | 1963 | 2692 | 1009 | 1145 |
| PCP | 3454 | 4154 | 3868 | 1941 | 2410 | 1042 | 1137 |
| PEV | 3584 | 3868 | 4154 | 1902 | 2590 | 1022 | 1098 |
| PS | 1963 | 1941 | 1902 | 4154 | 1697 | 1407 | 1296 |
| PAN | 2692 | 2410 | 2590 | 1697 | 4154 | 1360 | 1478 |
| PSD | 1009 | 1042 | 1022 | 1407 | 1360 | 4154 | 3071 |
| CDS-PP | 1145 | 1137 | 1098 | 1296 | 1478 | 3071 | 4154 |
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot()
sns.heatmap(
pv,
cmap=sns.color_palette("mako_r"),
linewidth=1,
annot = True,
square =True,
fmt="d",
cbar_kws={"shrink": 0.8})
plt.title('Iniciativas parlamentares: votos idênticos, XIII Leg.')
plt.show()
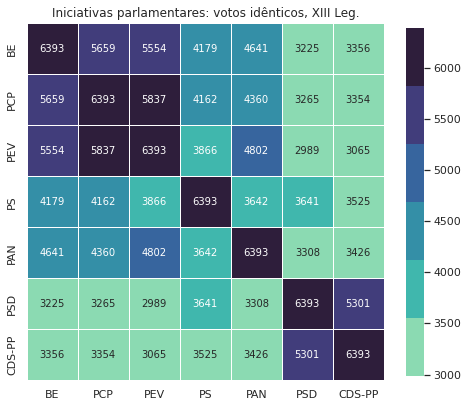
3.5. Matriz de distância e dendograma¶
Considerando a distância entre os votos (onde um voto a favor está mais perto de uma abstenção do que de um voto contra) obtemos o seguinte clustermap que conjuga a visualização da matriz de distância com o dendograma.
## Change the mapping, we now consider Abst and Aus the same
votes_hmn = votes_hm.replace(["A Favor", "Contra", "Abstenção", "Ausência"], [1,-1,0,0]).fillna(0)
## Transpose the dataframe used for the heatmap
votes_t = votes_hmn.transpose()
## Determine the Eucledian pairwise distance
## ("euclidean" is actually the default option)
pwdist = pdist(votes_t, metric='euclidean')
## Create a square dataframe with the pairwise distances: the distance matrix
distmat = pd.DataFrame(
squareform(pwdist), # pass a symmetric distance matrix
columns = votes_t.index,
index = votes_t.index
)
#show(distmat, scrollY="200px", scrollCollapse=True, paging=False)
## Normalise by scaling between 0-1, using dataframe max value to keep the symmetry.
## This is essentially a cosmetic step
#distmat=((distmat-distmat.min().min())/(distmat.max().max()-distmat.min().min()))*1
distmat.style.apply(highlight_diag, axis=None)
| BE | PCP | PEV | PS | PAN | PSD | CDS-PP | |
|---|---|---|---|---|---|---|---|
| BE | 0.000000 | 38.626416 | 35.665109 | 77.762459 | 54.212545 | 92.547285 | 90.983515 |
| PCP | 38.626416 | 0.000000 | 27.964263 | 76.752850 | 61.392182 | 91.394748 | 90.266273 |
| PEV | 35.665109 | 27.964263 | 0.000000 | 79.164386 | 54.616847 | 93.246984 | 92.671463 |
| PS | 77.762459 | 76.752850 | 79.164386 | 0.000000 | 77.961529 | 81.080207 | 83.839132 |
| PAN | 54.212545 | 61.392182 | 54.616847 | 77.961529 | 0.000000 | 81.449371 | 80.467385 |
| PSD | 92.547285 | 91.394748 | 93.246984 | 81.080207 | 81.449371 | 0.000000 | 43.439613 |
| CDS-PP | 90.983515 | 90.266273 | 92.671463 | 83.839132 | 80.467385 | 43.439613 | 0.000000 |
## Perform hierarchical linkage on the distance matrix using Ward's method.
distmat_link = hc.linkage(pwdist, method="ward", optimal_ordering=True )
sns.clustermap(
distmat,
annot = True,
cmap=sns.color_palette("Reds_r"),
linewidth=1,
#standard_scale=1,
row_linkage=distmat_link,
col_linkage=distmat_link,
figsize=(8,8)).fig.suptitle('Portuguese Parliament 13th Legislature, Clustermap',y=1)
plt.show()
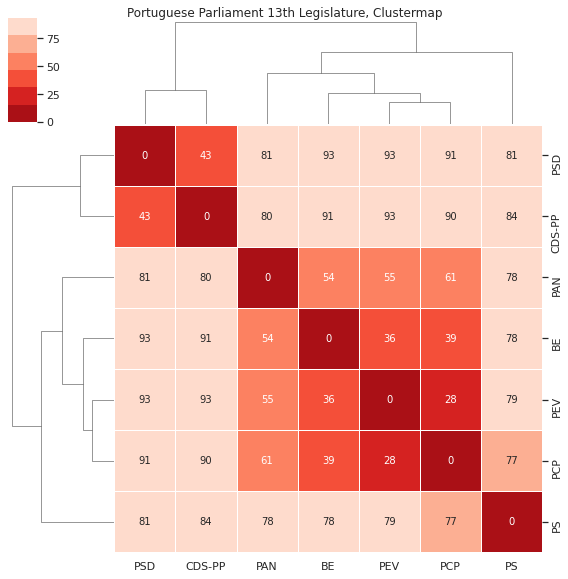
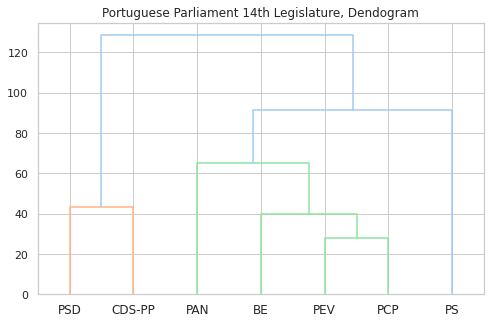
Parece clara a identificação de dois grande blocos: PSD e CDS-PP, e todos os outros - e dentro destes, o PS e o PAN mais próximos entre si, e PCP, PEV e BE próximos entre eles.
3.6. Clustering de observações: DBSCAN e Spectrum Scaling¶
Uma forma diferente de determinar agrupamentos é através de métodos de clustering, que procuram determinar agrupamentos de pontos com base em mecanismos específicos de cada um dos algoritmos.
Vamos demonstrar dois deles, e como passo preliminar vamos transformar a nossa matriz de distâncias: ao contrário do dendograma anterior estes métodos utilizam uma matriz de afinidade, onde valores mais altos significam uma maior semelhança (e, consequentemente, para uma matriz simétrica a diagonal passa de 0 para 1).
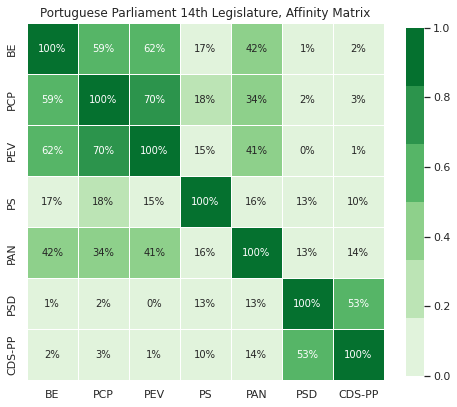
Como passo preliminar normalizamos as distâncias no intervalo [0,1], após o qual obtemos a matriz de afinidade a partir da matriz de distância:
distmat_mm=((distmat-distmat.min().min())/(distmat.max().max()-distmat.min().min()))*1
#pd.DataFrame(distmat_mm, distmat.index, distmat.columns)
affinmat_mm = pd.DataFrame(1-distmat_mm, distmat.index, distmat.columns)
affinmat_mm.style.apply(highlight_diag, axis=None)
| BE | PCP | PEV | PS | PAN | PSD | CDS-PP | |
|---|---|---|---|---|---|---|---|
| BE | 1.000000 | 0.585762 | 0.617520 | 0.166059 | 0.418613 | 0.007504 | 0.024274 |
| PCP | 0.585762 | 1.000000 | 0.700105 | 0.176887 | 0.341618 | 0.019864 | 0.031966 |
| PEV | 0.617520 | 0.700105 | 1.000000 | 0.151025 | 0.414278 | 0.000000 | 0.006172 |
| PS | 0.166059 | 0.176887 | 0.151025 | 1.000000 | 0.163924 | 0.130479 | 0.100892 |
| PAN | 0.418613 | 0.341618 | 0.414278 | 0.163924 | 1.000000 | 0.126520 | 0.137051 |
| PSD | 0.007504 | 0.019864 | 0.000000 | 0.130479 | 0.126520 | 1.000000 | 0.534145 |
| CDS-PP | 0.024274 | 0.031966 | 0.006172 | 0.100892 | 0.137051 | 0.534145 | 1.000000 |
3.6.1. DBSCAN¶
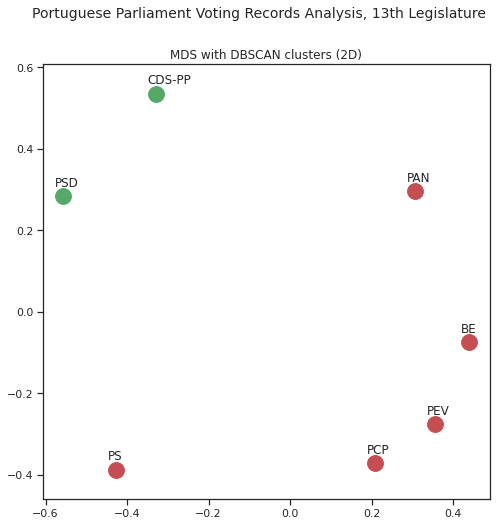
O DBSCAN é algoritmo que, entre outras características, não necessita de ser inicializado com um número pré-determinado de grupos, procedendo à sua identificação através da densidade dos pontos [DBS]: o DBSCAN identifica os grupos de forma automática.
from sklearn.cluster import DBSCAN
dbscan_labels = DBSCAN(eps=1.3).fit(affinmat_mm)
dbscan_labels.labels_
dbscan_dict = dict(zip(distmat_mm,dbscan_labels.labels_))
pd.DataFrame.from_dict(dbscan_dict, orient='index', columns=["Group"]).T
| BE | PCP | PEV | PS | PAN | PSD | CDS-PP | |
|---|---|---|---|---|---|---|---|
| Group | 0 | 0 | 0 | 0 | 0 | -1 | -1 |
Com DBSCAN identificamos 2 grupos: PSD e CDS-PP, e todos os restantes.
3.6.2. Spectral clustering¶
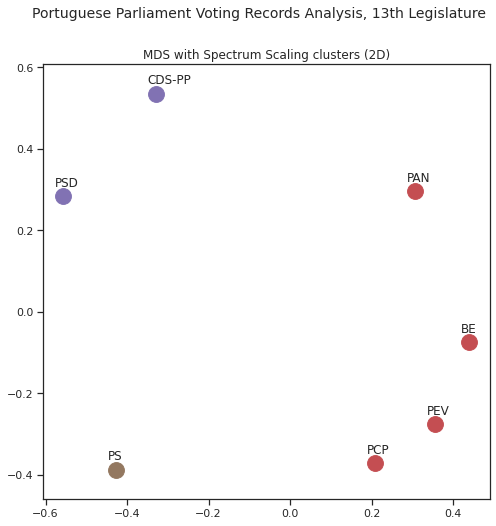
Outra abordagem para efectuar a identificação de grupos passa pela utilização de Spectral Clustering, uma forma de clustering que utiliza os valores-próprios e vectores-próprios de matrizes como forma de determinação dos grupos. Este método necessita que seja determinado a priori o número de clusters; assim, podemos usar este método para agrupamentos mais finos, neste caso identificando 3 grupos:
from sklearn.cluster import SpectralClustering
sc = SpectralClustering(3, affinity="precomputed",random_state=2020).fit_predict(affinmat_mm)
sc_dict = dict(zip(distmat,sc))
pd.DataFrame.from_dict(sc_dict, orient='index', columns=["Group"]).T
| BE | PCP | PEV | PS | PAN | PSD | CDS-PP | |
|---|---|---|---|---|---|---|---|
| Group | 0 | 0 | 0 | 2 | 0 | 1 | 1 |
Neste caso, e por determinarmos que devem existir 3 grupos, ao grupo anteriormente identificado por DBSCAN (PSD e CDS-PP) junta-se uma divisão entre PS (isolado) e os restantes. Esta divisão é compatível com os valores que observamos anteriormente.
3.6.3. Multidimensional scaling¶
Não temos ainda uma forma de visualizar a distância relativa de cada partido em relação aos outros com base nas distâncias/semelhanças: temos algo próximo com base no dendograma mas existem outras formas de visualização interessantes.
Uma das formas é o multidimensional scaling que permite visualizar a distância ao projectar em 2 ou 3 dimensões (também conhecidas como dimensões visualizavies) conjuntos multidimensionais, mantendo a distância relativa [ZWH15].
from sklearn.manifold import MDS
## Graphic options
sns.set()
sns.set_style("whitegrid")
fig, ax = plt.subplots(figsize=(8,8))
plt.title('Portuguese Parliament Voting Records Analysis, 13th Legislature', fontsize=14)
for label, x, y in zip(distmat_mm.columns, coords[:, 0], coords[:, 1]):
ax.scatter(x, y, s=250)
ax.axis('equal')
ax.annotate(label,xy = (x-0.02, y+0.025))
plt.show()
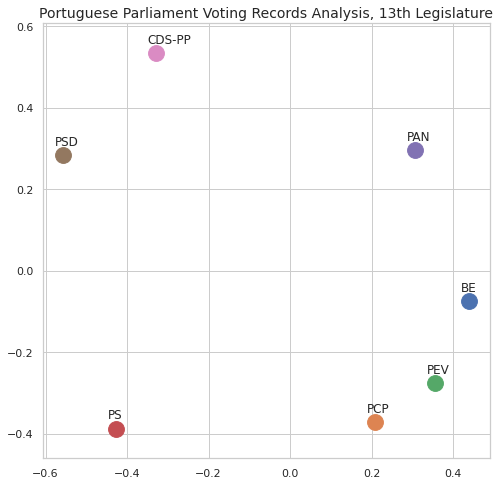
Por último, o mesmo MDS em 3D, e em forma interactiva:
mds = MDS(n_components=3, dissimilarity='precomputed',random_state=1234, n_init=100, max_iter=1000)
results = mds.fit(distmat.values)
parties = distmat.columns
coords = results.embedding_
import plotly.graph_objects as go
# Create figure
fig = go.Figure()
# Loop df columns and plot columns to the figure
for label, x, y, z in zip(parties, coords[:, 0], coords[:, 1], coords[:, 2]):
fig.add_trace(go.Scatter3d(x=[x], y=[y], z=[z],
text=label,
textposition="top center",
mode='markers+text', # 'lines' or 'markers'
name=label))
fig.update_layout(
width = 1000,
height = 1000,
title = "13th Legislature: 3D MDS",
template="plotly_white",
showlegend=False
)
fig.update_yaxes(
scaleanchor = "x",
scaleratio = 1,
)
plot(fig, filename = 'l13-3d-mds.html')
display(HTML('l13-3d-mds.html'))

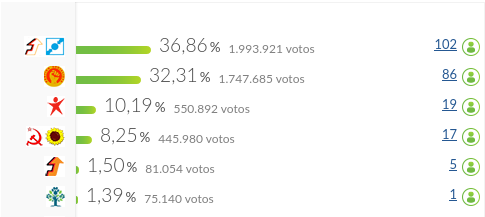 Fonte: CNE
Fonte: CNE