8. A XV Legislatura: os primeiros 6 meses¶
“O primeiro é breve, mas perigoso, atravessa vários obstáculos que só poderá evitar com muitíssimo trabalho; o outro mais largo, com margens, é plano e fácil se ajudar com magnetismo, não desvia nem à esquerda, nem à direita. O terceiro é certamente a via real: alguns prazeres e espetáculos de nosso Rei tornam seu caminho agradável. Mas apenas um dentre mil chegam por ele ao objetivo. Entretanto, pelo quarto nenhum homem pode chegar ao Palácio do Rei.”
—As Bodas Químicas de CR
8.1. Os primeiros meses da XV legislatura¶
As eleições legislativas realizadas em Janeiro de 2022 seguiram-se à dissolução da Assembleia da República, opção tomada pelo Presidente da República após a não aprovação do Orçamento de Estado para 2022. O governo minoritário do Partido Socialista governava desde 2015 com o apoio parlamentar dos partidos à sua esquerda, não tendo existido convergência suficient para assegurar a aprovação do Orçamento de Estado pelos votos contra de BE, PCP e PEV.
O resultado das eleições ditou uma maioria absoluta do PS, perdas substancias de BE, PCP e PAN, crescimento significativo de Chega e IL (ambos a constituirem grupo parlamentar), e a eleição de um deputado do Livre. CDS-PP não elege nenhum deputado, pela primeira vez, e PEV também não: ambos os partidos perdem a representação parlamentar.
Total de votações: 1296
Data limite inferior: 2022-04-22
Data limite superior: 2023-04-28
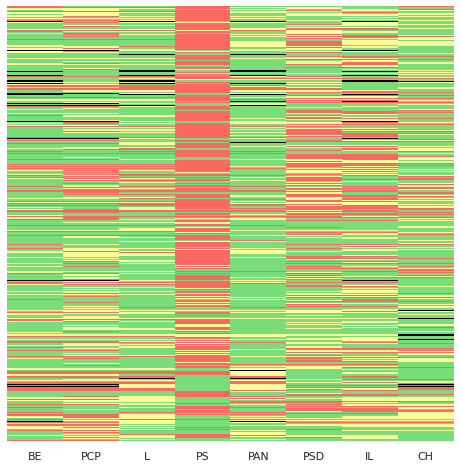
8.2. Mapa térmico das votações¶
O mapa térmico de votações para a legislatura – recordemos que nos permite ver através de cores todas as votações, dando uma imagem geral do comportamento dos vários partidos – é o seguinte:
votes_hmn = votes_hm.replace(["A Favor", "Contra", "Abstenção", "Ausência"], [1,-1,0,-2]).fillna(0)
##RYG
voting_palette = ["black","#FB6962","#FCFC99","#79DE79",]
fig = plt.figure(figsize=(8,8))
sns.heatmap(votes_hmn ,
square=False,
yticklabels = False,
cbar=False,
cmap=sns.color_palette(voting_palette),
linewidths=0,
)
plt.show()
8.3. Votações idênticas¶
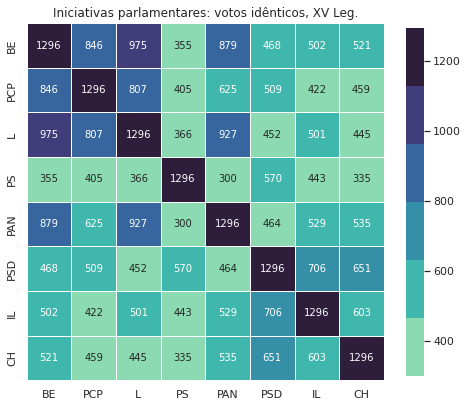
Das votações da legislatura é esta a matriz de votações idênticas:
pv_list = []
def highlight_diag(df):
a = np.full(df.shape, '', dtype='<U24')
np.fill_diagonal(a, 'font-weight: bold;')
return pd.DataFrame(a, index=df.index, columns=df.columns)
## Not necessarily the most straightforard way (check .crosstab or .pivot_table, possibly with pandas.melt and/or groupby)
## but follows the same approach as before in using a list of dicts
for party in votes_hm.columns:
pv_dict = collections.OrderedDict()
for column in votes_hmn:
pv_dict[column]=votes_hmn[votes_hmn[party] == votes_hmn[column]].shape[0]
pv_list.append(pv_dict)
pv = pd.DataFrame(pv_list,index=votes_hm.columns)
pv.style.apply(highlight_diag, axis=None)
| BE | PCP | L | PS | PAN | PSD | IL | CH | |
|---|---|---|---|---|---|---|---|---|
| BE | 1296 | 846 | 975 | 355 | 879 | 468 | 502 | 521 |
| PCP | 846 | 1296 | 807 | 405 | 625 | 509 | 422 | 459 |
| L | 975 | 807 | 1296 | 366 | 927 | 452 | 501 | 445 |
| PS | 355 | 405 | 366 | 1296 | 300 | 570 | 443 | 335 |
| PAN | 879 | 625 | 927 | 300 | 1296 | 464 | 529 | 535 |
| PSD | 468 | 509 | 452 | 570 | 464 | 1296 | 706 | 651 |
| IL | 502 | 422 | 501 | 443 | 529 | 706 | 1296 | 603 |
| CH | 521 | 459 | 445 | 335 | 535 | 651 | 603 | 1296 |
A visualização desta matriz através de um mapa térmico:
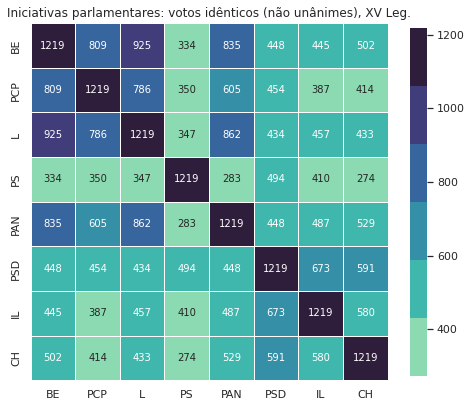
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot()
sns.heatmap(
pv,
cmap=sns.color_palette("mako_r"),
linewidth=1,
annot = True,
square =True,
fmt="d",
cbar_kws={"shrink": 0.8})
plt.title('Iniciativas parlamentares: votos idênticos, XV Leg.')
plt.show()
8.4. Matriz de distância e dendograma¶
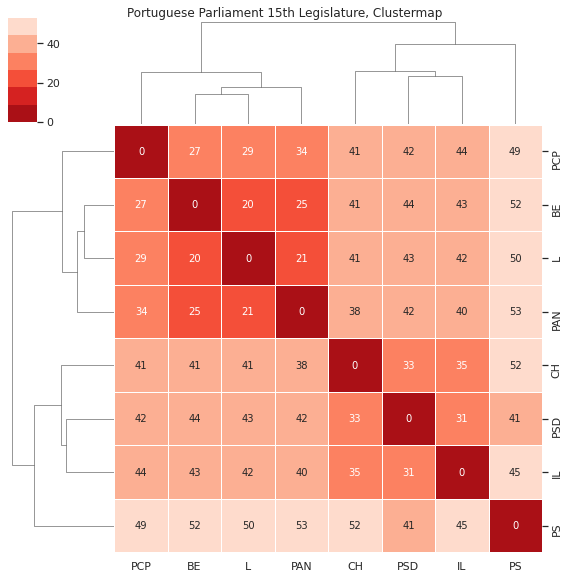
Considerando a distância entre os votos (onde um voto a favor está mais perto de uma abstenção do que de um voto contra) obtemos o seguinte clustermap que conjuga a visualização da matriz de distância com o dendograma: como se relacionam os partidos e como se agrupam com base nos seus votos.
O clustermap inclui os resultados do agrupamentos pelo método de Ward, com base nas distâncias acima:
## Perform hierarchical linkage on the distance matrix using Ward's method.
distmat_link = hc.linkage(pwdist, method="ward", optimal_ordering=True )
sns.clustermap(
distmat,
annot = True,
cmap=sns.color_palette("Reds_r"),
linewidth=1,
#standard_scale=1,
row_linkage=distmat_link,
col_linkage=distmat_link,
figsize=(8,8)).fig.suptitle('Portuguese Parliament 15th Legislature, Clustermap',y=1)
plt.show()
8.5. Clustering de observações: Spectrum Scaling¶
Uma forma diferente de determinar agrupamentos é através de métodos de clustering, que procuram determinar agrupamentos de pontos com base em mecanismos específicos de cada um dos algoritmos.
Spectral Clustering é uma forma de clustering que utiliza os valores-próprios e vectores-próprios de matrizes como forma de determinação dos grupos. Este método necessita que seja determinado a priori o número de clusters; assim, podemos usar este método para agrupamentos mais finos.
from sklearn.cluster import SpectralClustering
sc = SpectralClustering(4, affinity="precomputed",random_state=2020).fit_predict(affinmat_mm)
sc_dict = dict(zip(distmat,sc))
pd.DataFrame.from_dict(sc_dict, orient='index', columns=["Group"]).T
| BE | PCP | L | PS | PAN | PSD | IL | CH | |
|---|---|---|---|---|---|---|---|---|
| Group | 1 | 3 | 1 | 0 | 1 | 2 | 2 | 2 |
8.5.1. Multidimensional scaling¶
Não temos ainda uma forma de visualizar a distância relativa de cada partido em relação aos outros com base nas distâncias/semelhanças: temos algo próximo com base no dendograma mas existem outras formas de visualização interessantes.
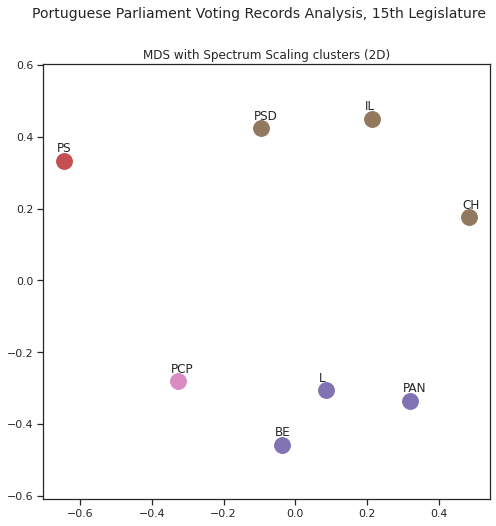
Uma das formas é o multidimensional scaling que permite visualizar a distância ao projectar em 2 ou 3 dimensões (também conhecidas como dimensões visualizavies) conjuntos multidimensionais, mantendo a distância relativa [ZWH15]. Juntando à representação cores que representam o agrupamento feito por Spectrum Clustering temos o seguinte resultado:
from sklearn.manifold import MDS
import random
mds = MDS(n_components=2, dissimilarity='precomputed',random_state=2020, n_init=100, max_iter=1000)
## We use the normalised distance matrix but results would
## be similar with the original one, just with a different scale/axis
results = mds.fit(distmat_mm.values)
coords = results.embedding_
sns.set()
sns.set_style("ticks")
fig, ax = plt.subplots(figsize=(8,8))
fig.suptitle('Portuguese Parliament Voting Records Analysis, 15th Legislature', fontsize=14)
ax.set_title('MDS with Spectrum Scaling clusters (2D)')
for label, x, y in zip(distmat_mm.columns, coords[:, 0], coords[:, 1]):
ax.scatter(x, y, c = "C"+str(sc_dict[label]+3
), s=250)
ax.axis('equal')
ax.annotate(label,xy = (x-0.02, y+0.025))
plt.show()
#glue("mds_15", fig, display=False)
Por último, o mesmo MDS em 3D, e em forma interactiva:
mds = MDS(n_components=3, dissimilarity='precomputed',random_state=1234, n_init=100, max_iter=1000)
results = mds.fit(distmat.values)
parties = distmat.columns
coords = results.embedding_
import plotly.graph_objects as go
# Create figure
fig = go.Figure()
# Loop df columns and plot columns to the figure
for label, x, y, z in zip(parties, coords[:, 0], coords[:, 1], coords[:, 2]):
fig.add_trace(go.Scatter3d(x=[x], y=[y], z=[z],
text=label,
textposition="top center",
mode='markers+text', # 'lines' or 'markers'
name=label))
fig.update_layout(
width = 1000,
height = 1000,
title = "15th Legislature: 3D MDS",
template="plotly_white",
showlegend=False
)
fig.update_yaxes(
scaleanchor = "x",
scaleratio = 1,
)
fig.write_html('l15-3d-mds.html')
display(HTML('l15-3d-mds.html'))
8.6. Propostas apresentadas: quem aprova as propostas de quem.¶
Utilizámos a mesma abordagem já detalhada em pormenor em análises da XIV legislatura, para a qual remetemos para mais detalhes. De forma resumida, a análise é feito com base nas propostas votadas na generalidade - e apenas essas - e das quais se obtem o partido que apresenta a iniciativa, e os votos dos restantes.
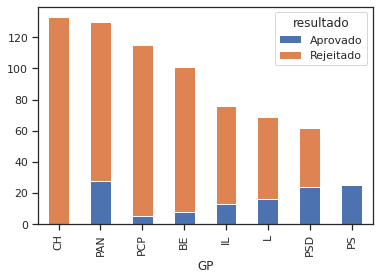
O total de propostas votadas na generalidade, com a identificação das aprovadas e rejeitadas, é o seguinte:
ct = pd.crosstab(l15af.GP, l15af.resultado)
ct["Total"] = ct["Aprovado"] + ct["Rejeitado"]
ct.sort_values(by=['Total'], axis=0, ascending=False)
| resultado | Aprovado | Rejeitado | Total |
|---|---|---|---|
| GP | |||
| CH | 0 | 133 | 133 |
| PAN | 28 | 102 | 130 |
| PCP | 5 | 110 | 115 |
| BE | 8 | 93 | 101 |
| IL | 13 | 63 | 76 |
| L | 16 | 53 | 69 |
| PSD | 24 | 38 | 62 |
| PS | 25 | 0 | 25 |
Podemos também visualizar a quantidade de propostas aprovadas e rejeitadas:
ct.sort_values(by=['Total'], axis=0, ascending=False).drop("Total", axis=1).plot(kind="bar", stacked=True)
plt.show()
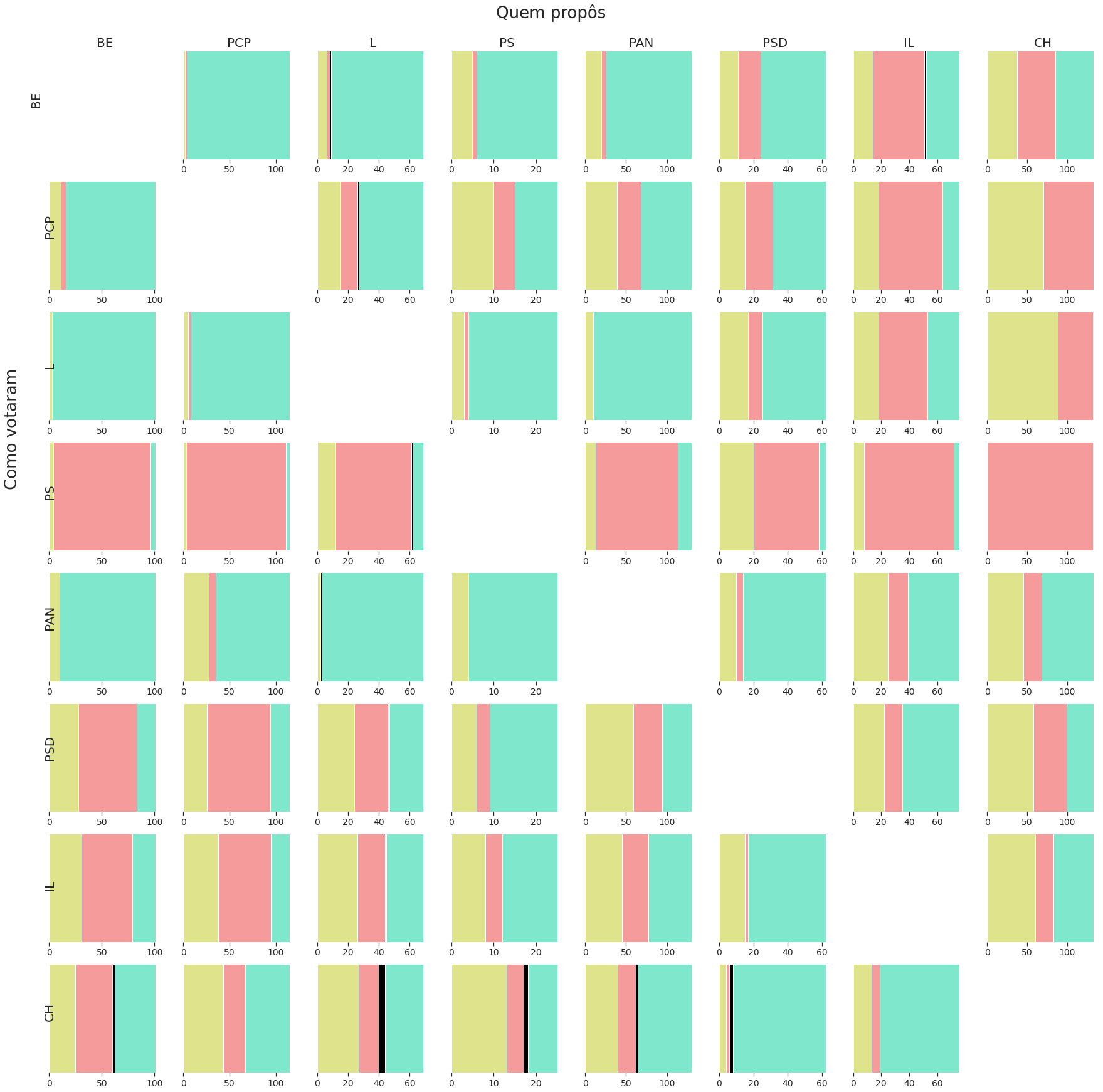
Com esta informação, e de forma muito semelhante à utilizada para determinar os apoios às propostas de alteração do Orçamento de Estado, é possível determinar os padrões de votação; o diagrama seguinte mostra a relação entre cada par de partidos: no eixo horizontal quem propõe, e no vertical como votaram:
import seaborn as sns
from matplotlib.colors import ListedColormap
#parties = ['BE', 'PCP', 'PEV', 'PS', 'L', 'PAN','PSD','IL','CDS-PP', 'CH']
#parties = ['BE', 'PCP','PS', 'PAN','PSD','IL','CDS-PP', 'CH']
parties = ['BE', 'PCP', 'L', 'PS', 'PAN','PSD','IL', 'CH' ]
gpsubs = submissions_ini
cmap=ListedColormap(sns.color_palette("pastel").as_hex())
colors=["#DFE38C","#F59B9B","black","#7FE7CC" ]
cmap = ListedColormap(colors)
spn = 0
fig, axes = plt.subplots(nrows=8, ncols=8, figsize=(30, 30))
axes = axes.ravel()
plt.rcParams.update({'font.size': 22})
for party in parties:
for p2 in parties:
sns.set_style("white")
subp = gpsubs[gpsubs['GP'] == p2][[party]]
sp = subp.fillna("Ausência").apply(pd.Series.value_counts)
d = pd.DataFrame(columns=["GP","Abstenção", "Contra", "Ausência","A Favor"]).merge(sp.T, how="right").fillna(0)
d["GP"] = party
d = d.set_index("GP")
d = d[["Abstenção", "Contra", "Ausência","A Favor"]]
if p2 != party:
sns.despine(left=True, bottom=True)
if spn < 8:
d.plot(kind='barh', stacked=True,width=400,colormap=cmap, title=p2,use_index=False,ax=axes[spn], fontsize=12)
axes[spn].title.set_size(20)
else:
d.plot(kind='barh', stacked=True,width=400,colormap=cmap,use_index=False,ax=axes[spn])
axes[spn].get_legend().remove()
plt.ylim(-4.5, axes[spn].get_yticks()[-1] + 0.5)
axes[spn].tick_params(labelsize=14)
else:
axes[spn].set_xticks([])
#d.plot(kind='barh', stacked=True,width=400,colormap=cmap,use_index=False,ax=axes[spn])
#axes[spn].get_legend().remove()
if spn < 7:
axes[spn].set_title(p2, fontsize=20)
axes[spn].set_yticks([])
## Why? Who knows? Certainly not me. This is likely a side-effect of using a single axis through .ravel
if spn%8 == 0:
if spn != 0:
text = axes[spn].text(-5,0,party,rotation=90, fontsize=20)
else:
text = axes[spn].text(-0.17,0.5,party,rotation=90,fontsize=20)
#print(party, p2)
#print(d)
#print("-------------------------_")
spn += 1
#axes[11].set_axis_off()
text = axes[0].text(4,1.3,"Quem propôs",rotation=0,fontsize=26)
text = axes[0].text(-0.4,-3,"Como votaram",rotation=90,fontsize=26)
#fig.tight_layout()
plt.show()
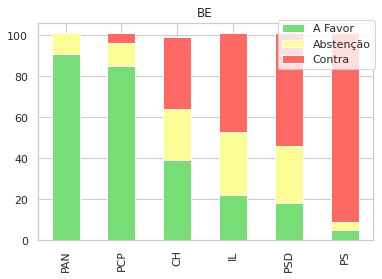
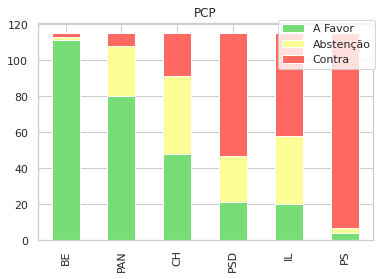
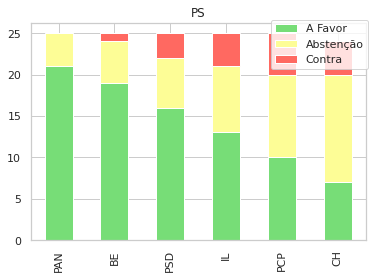
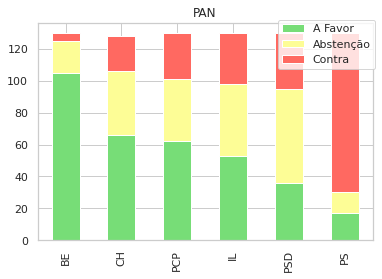
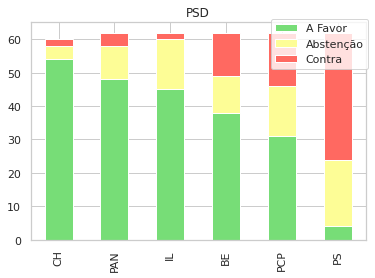
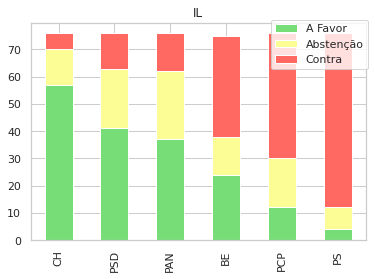
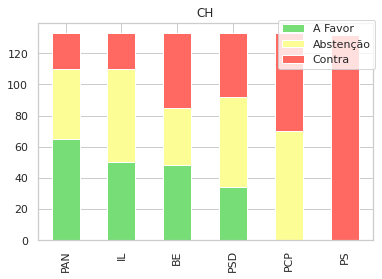
Uma outra visualização que foca cada gráfico nas propostas de cada partido, e como votaram os restantes:
from IPython.display import display
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
from matplotlib import cm
parties = ['BE', 'PCP', 'PEV', 'PS'
, 'PAN','PSD','IL','CDS-PP', 'CH']
parties = ['BE', 'PCP', 'PS', 'PAN','PSD','IL', 'CH' ]
ndf = pd.DataFrame()
#submissions_ini_nu = submissions_ini.loc[submissions_ini['unanime'] != "unanime"]
gpsubs = submissions_ini
cmap=ListedColormap(sns.color_palette("pastel").as_hex())
colors=["#77dd77","#fdfd96","#ff6961", ]
cmap = ListedColormap(colors)
#spn = 0
#axes = axes.ravel()
for party in parties:
sns.set_style("whitegrid")
subp = gpsubs[gpsubs['GP'] == party]
sp = subp[parties].apply(pd.Series.value_counts).fillna(0).drop([party],axis=1)
sp = sp.sort_values(by=['A Favor','Abstenção','Contra'], ascending=False, axis=1)
d = sp.T
f = plt.figure()
plt.title(party)
d.plot(kind='bar', ax=f.gca(), stacked=True, title=party, colormap=cmap,)
plt.legend(loc='center left', bbox_to_anchor=(0.7, 0.9),)
plt.show()
#print(d)
plt.show()