2. Metodologia e resultados: visão geral¶
Com base nos dados disponibilizados pela Assembleia da República em formato XML são criadas dataframes (tabelas de duas dimensões) com base no processamento e selecção de informação relativa aos padrões de votação de cada partido (e/ou deputados não-inscritos).
Uma explicação mais detalhada dos processos pode ser obtida nos apêndices, o que se segue é uma introdução a algumas das análises fundamentais com base num exemplo fictício.
2.1. As votações e os partidos¶
Para simplificar usamos desde já valores numéricos, onde 1 = Favor, 0 = Abstenção, -1 = Contra, e não consideramos ausências. O processo de tratamento de dados reais irá, num dos seus passos, fazer esta transformação.
Considerem-se 4 partidos, para o nosso efeito denominados pelo sentido mais comum do seu voto; a seguinte tabela reflecte 10 votações e o comportamente de cada partido em cada uma delas
v5=[[1,1,1,1,1,1,1,1,1,1],[0,0,0,0,0,0,0,0,0,0],[1,0,0,0,1,1,0,1,0,1],[-1,-1,-1,-1,-1,-1,-1,-1,-1,-1]]
v5_df = pd.DataFrame(v5, columns=["v1","v2", "v3","v4","v5","v6","v7","v8","v9","v10"], index=["Fav","Abst","Var","Cont"])
v5_df
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 | v10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Fav | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Abst | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Var | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| Cont | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
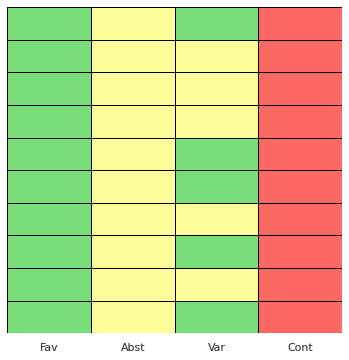
2.2. Mapa térmico das votações de todos os partidos¶
Um mapa térmico permite-nos visualizar os votos através de cores; é uma forma de observar os mesmos dados que os da tabela mas de forma gráfica, o que se neste caso não faz muita diferenças, passa a ser importante quando temos centenas de votações.
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
voting_palette = ["#FB6962","#FCFC99","#79DE79"]
fig = plt.figure(figsize=(6,6))
sns.heatmap(v5_df.T,
square=False,
yticklabels = False,
cbar=False,
cmap=sns.color_palette(voting_palette),
linecolor="black",
linewidths=1
)
plt.show()
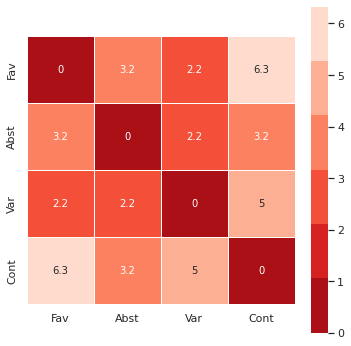
2.3. Matriz de distância¶
Uma matriz de distância apresenta o resultado das distâncias entre dois pontos - é o formato usado, por exemplo, para mostrar a distância entre vários pontos geográficos.
No caso de partidos e votações a distância é o resultado das diferenças entre sentidos de votos acumulados para todas as votações (de forma muito simples), e representada por uma matriz bidimensional onde quanto maior o número, mais distante está do par correspondente.
v5_distmat=pd.DataFrame(squareform(pdist(v5)), columns=v5_df.index, index=v5_df.index)
v5_distmat
| Fav | Abst | Var | Cont | |
|---|---|---|---|---|
| Fav | 0.000000 | 3.162278 | 2.236068 | 6.324555 |
| Abst | 3.162278 | 0.000000 | 2.236068 | 3.162278 |
| Var | 2.236068 | 2.236068 | 0.000000 | 5.000000 |
| Cont | 6.324555 | 3.162278 | 5.000000 | 0.000000 |
A sua visualização (também através de um mapa térmico) permite ver rapidamente as proximidades através das cores utilizadas: quanto mais claro, mais distante.
plt.figure(figsize=(6,6))
sns.heatmap(
v5_distmat,
cmap=sns.color_palette("Reds_r"),
linewidth=1,
annot = True,
square =True,
)
plt.show()
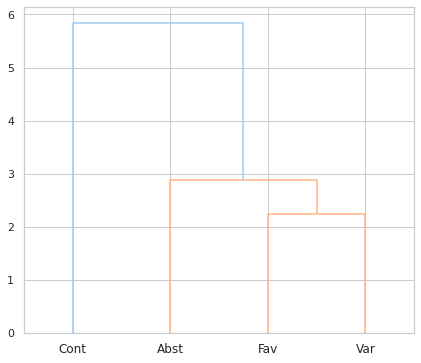
2.4. Dendograma e clustermap¶
Com base nas distâncias segue-se o agrupamento (clustering); existem várias formas de o fazer e é preciso ter em consideração que o resultado obtido considera as distâncias entre todos os pares: é perfeitamente possível que elementos com maior distância aparecem agrupados de forma mais próxima devido à distância que cada um deles tem de todos os outros.
Dito isto, a visualização mais comum é um dendograma que apresenta uma “árvore” com diferentes ramos:
v5_distmat_link = hc.linkage(pdist(v5_df), method="ward")
from scipy.cluster.hierarchy import dendrogram
fig = plt.figure(figsize=(7,6))
dendrogram(v5_distmat_link, labels=v5_df.T.columns)
plt.show()
Um clustermap é a combinação do mapa térmico de distância com o dendograma: as colunas e linhas são reordernadas e as linhas de agrupamento adicionadas.
sns.clustermap(
v5_distmat,
annot = True,
cmap=sns.color_palette("Reds_r"),
linewidth=1,
row_linkage=v5_distmat_link,
col_linkage=v5_distmat_link,
figsize=(6,6)
)
plt.title('Clustermap')
plt.show()
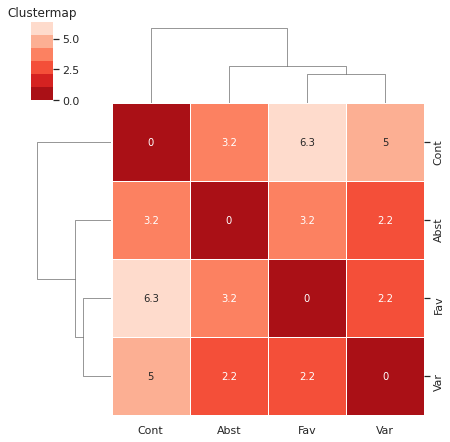
Como o clustermap combina a informação de ambos será o mais utilizado.
2.5. Multidimensional Scaling¶
Com base na matriz de distâncias podemos também visulizar a distância relativa entre todos os partidos através de Multidimensional scaling: com base na distância (acumulada) entre todos os pares determinam-se coordenadas em duas ou três dimensões (daí o nome, trata-se de reduzir as dimensões mantendo a distância relativa)
from sklearn.manifold import MDS
import random
mds = MDS(n_components=2, dissimilarity='precomputed',random_state=2020, n_init=100, max_iter=1000)
results = mds.fit(v5_distmat.values)
coords = results.embedding_
fig, ax = plt.subplots(figsize=(8,8))
for label, x, y in zip(v5_distmat.columns, coords[:, 0], coords[:, 1]):
ax.scatter(x, y, s=250)
ax.axis('equal')
ax.annotate(
label,
xy = (x+0.1, y),
)
plt.show()
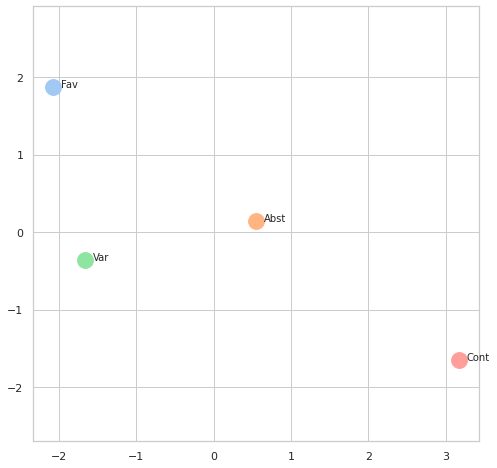
Observe-se que não temos agrupamentos: MDS não é um método de clustering mas sim de redução das dimensões de forma a manter as distâncias relativas entre os vários pontos, o que nos permite identificar visualmente possíveis grupos (e, neste caso, podemos ver como se relaciona com a matriz de distância obtida anteriormente). A redução das dimensões pode ser feita para 2 ou para 3, sendo nesse caso o resultado visualizável num cubo:
from sklearn.manifold import MDS
import random
mds = MDS(n_components=3, dissimilarity='precomputed',random_state=2020, n_init=100, max_iter=1000)
results = mds.fit(v5_distmat.values)
coords = results.embedding_
import plotly.graph_objects as go
from IPython.core.display import display, HTML
from plotly.offline import init_notebook_mode, plot
init_notebook_mode(connected=True)
# Create figure
fig = go.Figure()
# Loop df columns and plot columns to the figure
for label, x, y, z in zip(v5_df.T.columns, coords[:, 0], coords[:, 1], coords[:, 2]):
fig.add_trace(go.Scatter3d(x=[x], y=[y], z=[z],
text=label,
textposition="top center",
mode='markers+text', # 'lines' or 'markers'
name=label))
fig.update_layout(
width = 800,
height = 800,
scene_aspectmode='cube',
title = "3D MDS",
template="plotly_white",
showlegend=False
)
plot(fig, filename = 'intro_3d_mds.html')
display(HTML('intro_3d_mds.html'))
