Contents

4. Continuidade e fim: a XIV Legislatura

Alguns tinham ganho a partida, outros tinham perdido. Muitos tinham vindo buscar dor, outros a honra e a glória. Mas agora é tempo de os apartar - ninguém aqui consegue ver coisa nenhuma!

—Wolfram von Eschenback, «Parsival»

4.1. As eleições legislativas de 2019

Resultados eleitorias das legislativas de 2019

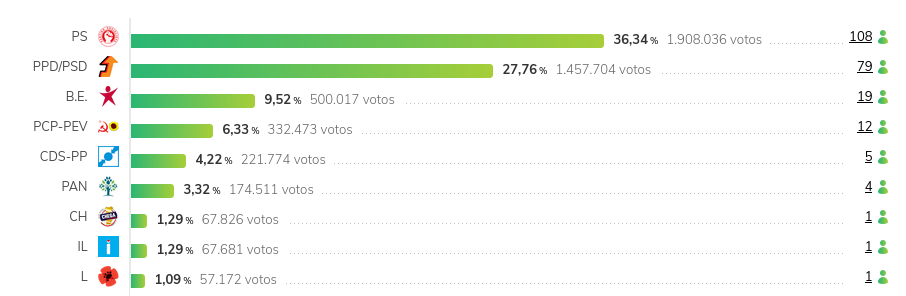
fishy Fonte: CNE [CNEb]

A XIV Legislatura resultou das eleições legislativas de 2019. Estas eleições são marcadas pela subida do PS (no Governo) e perdas de praticamente todos os partidos: sem impacto no número dos deputados, no caso do BE, mas com impacto significativo no caso da CDU (que perde 10 deputados). Á direita, o CDS-PP perde 13 deputados e o PSD 10.

É uma legislatura marcada pelo crescimento de partidos recentes que já tinham representação parlamentar (o caso do PAN, que sobe de 1 para 3 deputados) e sobretudo pela estreia de dois partidos na Assembleia: a Iniciativa Liberal, o CHEGA e o Livre, ambos com 1 deputado.

Deputadas não-inscritas

No decorrer da legislatura iriam acontecer cisões dentro do PAN e do Livre: no caso do PAN a deputada Cristina Rodrigues desfilia-se e sai do grupo parlamentar do PAN (que continha a existir com os restantes deputados). No caso do Livre, Joacine Katar Moreira quebra a sua ligação com o partido e passa à condição de deputada não-inscrita, deixando de haver representação do Livre no Parlamento. Estes acontecimentos têm importância para o tratamento dos dados.

4.2. Os dados das votações

Para a XIV legislatura os dados analisados podem incluir tanto Iniciativas como Actividades; de forma a manter uma uniformidade com os dados da XIII licenciatura irão ser usados, na análise principal, apenas os dados das Iniciativas, sendo os dados isolados ou agregados das Actividades analisados à margem.

Votos “não políticos”?

Um tema que (com alguma surpresa) surgiu aquando da publicação da análise inicial (que agrupava Iniciativas e Actividades, e também as várias combinações isoladas) foi o de que votações sobre votos de pesar, condenação ou congratulação não são “políticos”; tendo em conta a quantidade nada desprezável de votos desse tipo com posições diferentes dos vários partidos, a alternativa a serem votos políticos é uma incógnita: a não aprovação de um voto de pesar ou condenação significaria não um posicionamento político sobre o texto (que é diferente do acontecimento em si), mas algo de pessoal ou moral. Como veremos, estes votos têm uma distribuição e padrão próprios.

Estatísticas base

Os dados essenciais do ficheiro XML importado são as seguintes:

Total de votações: 3746

Data limite inferior: 2019-10-25

Data limite superior: 2021-10-27

O processamento inicial resulta num conjunto bastante alargado de colunas e observações (votações, uma por linha), nomeadamente os votos dos vários partidos; as deputadas independentes Joacina Katar Moreira e Cristina Rodrigues têm os seus votos complementados pelos do partido de origem.

Os votos após cisões

A referida saída de duas deputadas dos partidos pelos quais foram eleitos levam à necessidade de definir uma abordagem para a contabilização dos votos. A solução adoptada foi a de considerar que o histórico de votos das deputadas inclui o sentido de voto do partido antes da sua saída. Para o caso de Joacine Katar Moreira, deputada única, esta opção é transparente. No caso de Cristina Rodrigues o grupo parlamentar do PAN continua a existir após a sua saída, mas cremos que a mesma solução é a que mais faz sentido.

with pd.option_context("display.max_columns", 0):
    display(votes[["resultado", "id"] + parties])
resultado id BE PCP PEV L/JKM PS PAN PAN/CR PSD IL CDS-PP CH
0 Aprovado 88184 Contra Contra Contra Contra A Favor Contra Contra A Favor Abstenção Contra Contra
1 Aprovado 88183 Contra Contra Contra Contra A Favor Contra Contra A Favor Abstenção Contra Contra
2 Aprovado 88181 Contra Contra Contra Contra A Favor Contra Contra A Favor Abstenção Contra Contra
3 Aprovado 87725 A Favor A Favor A Favor A Favor Contra A Favor A Favor A Favor A Favor A Favor A Favor
4 Aprovado 88346 A Favor A Favor A Favor A Favor Contra A Favor A Favor A Favor A Favor A Favor A Favor
... ... ... ... ... ... ... ... ... ... ... ... ... ...
3741 Aprovado 92037 A Favor A Favor A Favor A Favor Abstenção A Favor A Favor A Favor A Favor A Favor A Favor
3742 Aprovado 91922 A Favor Ausência NaN NaN A Favor A Favor A Favor A Favor NaN A Favor NaN
3743 Rejeitado 92026 Contra Contra Contra Abstenção A Favor Abstenção Abstenção Contra Contra Contra Contra
3744 Aprovado 91915 A Favor NaN NaN NaN A Favor NaN NaN A Favor NaN A Favor NaN
3745 Aprovado 91916 A Favor NaN NaN NaN A Favor NaN NaN A Favor NaN A Favor NaN

3746 rows × 13 columns

4.3. Mapa térmico das votações

O mapa térmico de votações para a legislatura – recordemos que nos permite ver através de cores todas as votações, dando uma imagem geral do comportamento dos vários partidos – é o seguinte:

votes_hmn = votes_hm.replace(["A Favor", "Contra", "Abstenção", "Ausência"], [1,-1,0,-2]).fillna(0)

##RYG
voting_palette = ["black","#FB6962","#FCFC99","#79DE79",]

fig = plt.figure(figsize=(8,8))
sns.heatmap(votes_hmn ,
            square=False,
            yticklabels = False,
            cbar=False,
            cmap=sns.color_palette(voting_palette),
            linewidths=0,
           )
plt.show()
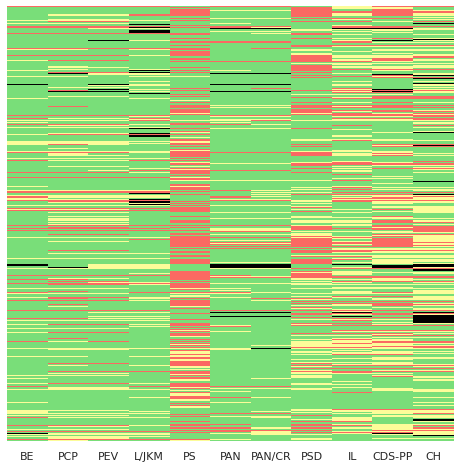
_images/l14_26_0.png

4.4. Votações idênticas

Das votações da legislatura é esta a matriz de votações idênticas:

pv_list = []
def highlight_diag(df):
    a = np.full(df.shape, '', dtype='<U24')
    np.fill_diagonal(a, 'font-weight: bold;')
    return pd.DataFrame(a, index=df.index, columns=df.columns)

## Not necessarily the most straightforard way (check .crosstab or .pivot_table, possibly with pandas.melt and/or groupby)
## but follows the same approach as before in using a list of dicts
for party in votes_hm.columns:
    pv_dict = collections.OrderedDict()
    for column in votes_hmn:
        pv_dict[column]=votes_hmn[votes_hmn[party] == votes_hmn[column]].shape[0]
    pv_list.append(pv_dict)

pv = pd.DataFrame(pv_list,index=votes_hm.columns)
pv.style.apply(highlight_diag, axis=None)
  BE PCP PEV L/JKM PS PAN PAN/CR PSD IL CDS-PP CH
BE 3746 2987 3024 3107 1582 2844 2807 1848 1762 1809 1673
PCP 2987 3746 3467 2749 1522 2416 2448 1843 1753 1768 1656
PEV 3024 3467 3746 2912 1451 2516 2542 1746 1769 1693 1658
L/JKM 3107 2749 2912 3746 1400 2734 2798 1680 1814 1668 1643
PS 1582 1522 1451 1400 3746 1593 1554 2221 1564 1705 1128
PAN 2844 2416 2516 2734 1593 3746 3385 1918 1977 1911 1747
PAN/CR 2807 2448 2542 2798 1554 3385 3746 1955 1985 1903 1773
PSD 1848 1843 1746 1680 2221 1918 1955 3746 2116 2548 1927
IL 1762 1753 1769 1814 1564 1977 1985 2116 3746 2241 2157
CDS-PP 1809 1768 1693 1668 1705 1911 1903 2548 2241 3746 2202
CH 1673 1656 1658 1643 1128 1747 1773 1927 2157 2202 3746

Votos idênticos vs. distância de votos

Este quadro parece ser um dos mais populares, talvez por ser muito directo na mensagem que transmite. Por isso mesmo fica a nota: a consideração apenas dos votos “idênticos” desconsidera completamente a diferença entre votar Contra e Abstenção. Esta dimensão irá ser capturada na matriz de distâncias.

A visualização desta matriz através de um mapa térmico:

Votos unânimes

Removendo os votos unânimes pode-se obter um mapa térmico semelhante, mas com uma escala diferente. Não há alteração substantiva ao anterior, nem a remoção dos votos unânimes altera as distâncias.

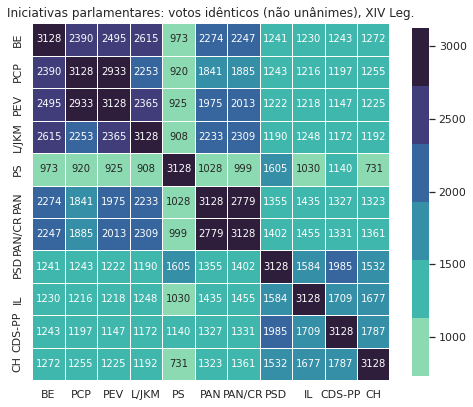
_images/l14_32_0.png

A tabela respectiva (observe-se o menor número de votações consideradas, dada a remoção das unânimes)

  BE PCP PEV L/JKM PS PAN PAN/CR PSD IL CDS-PP CH
BE 3128 2390 2495 2615 973 2274 2247 1241 1230 1243 1272
PCP 2390 3128 2933 2253 920 1841 1885 1243 1216 1197 1255
PEV 2495 2933 3128 2365 925 1975 2013 1222 1218 1147 1225
L/JKM 2615 2253 2365 3128 908 2233 2309 1190 1248 1172 1192
PS 973 920 925 908 3128 1028 999 1605 1030 1140 731
PAN 2274 1841 1975 2233 1028 3128 2779 1355 1435 1327 1323
PAN/CR 2247 1885 2013 2309 999 2779 3128 1402 1455 1331 1361
PSD 1241 1243 1222 1190 1605 1355 1402 3128 1584 1985 1532
IL 1230 1216 1218 1248 1030 1435 1455 1584 3128 1709 1677
CDS-PP 1243 1197 1147 1172 1140 1327 1331 1985 1709 3128 1787
CH 1272 1255 1225 1192 731 1323 1361 1532 1677 1787 3128 
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot()

sns.heatmap(
    pv,
    cmap=sns.color_palette("mako_r"),
    linewidth=1,
    annot = True,
    square =True,
    fmt="d",
    cbar_kws={"shrink": 0.8})
plt.title('Iniciativas parlamentares: votos idênticos, XIV Leg.')

plt.show()
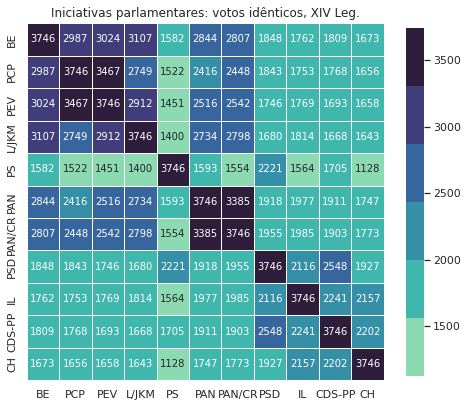
_images/l14_35_0.png

4.5. Matriz de distância e dendograma

Considerando a distância entre os votos (onde um voto a favor está mais perto de uma abstenção do que de um voto contra) obtemos o seguinte clustermap que conjuga a visualização da matriz de distância com o dendograma.

## Change the mapping, we now consider Abst and Aus the same
votes_hmn = votes_hm.replace(["A Favor", "Contra", "Abstenção", "Ausência"], [1,-1,0,0]).fillna(0)

## Transpose the dataframe used for the heatmap
votes_t = votes_hmn.transpose()

## Determine the Eucledian pairwise distance
## ("euclidean" is actually the default option)
pwdist = pdist(votes_t, metric='euclidean')

## Create a square dataframe with the pairwise distances: the distance matrix
distmat = pd.DataFrame(
    squareform(pwdist), # pass a symmetric distance matrix
    columns = votes_t.index,
    index = votes_t.index
)
#show(distmat, scrollY="200px", scrollCollapse=True, paging=False)

## Normalise by scaling between 0-1, using dataframe max value to keep the symmetry.
## This is essentially a cosmetic step
#distmat=((distmat-distmat.min().min())/(distmat.max().max()-distmat.min().min()))*1
    
distmat.style.apply(highlight_diag, axis=None)
  BE PCP PEV L/JKM PS PAN PAN/CR PSD IL CDS-PP CH
BE 0.000000 37.682887 33.719431 27.676705 79.956238 40.521599 40.509258 71.826179 64.202804 67.438861 59.665736
PCP 37.682887 0.000000 21.470911 40.224371 77.852424 52.249402 50.487622 67.712628 63.545259 65.620119 58.068925
PEV 33.719431 21.470911 0.000000 34.568772 78.917679 48.466483 46.690470 69.382995 63.568860 67.282984 58.557664
L/JKM 27.676705 40.224371 34.568772 0.000000 79.856121 40.049969 38.301436 71.407283 62.032250 66.843100 58.343809
PS 79.956238 77.852424 78.917679 79.856121 0.000000 78.885994 78.587531 58.770741 68.636725 66.294796 72.173402
PAN 40.521599 52.249402 48.466483 40.049969 78.885994 0.000000 22.956481 68.607580 58.086143 63.545259 56.639209
PAN/CR 40.509258 50.487622 46.690470 38.301436 78.587531 22.956481 0.000000 66.813172 56.982453 63.047601 55.506756
PSD 71.826179 67.712628 69.382995 71.407283 58.770741 68.607580 66.813172 0.000000 54.616847 45.000000 53.075418
IL 64.202804 63.545259 63.568860 62.032250 68.636725 58.086143 56.982453 54.616847 0.000000 47.370877 47.010637
CDS-PP 67.438861 65.620119 67.282984 66.843100 66.294796 63.545259 63.047601 45.000000 47.370877 0.000000 43.497126
CH 59.665736 58.068925 58.557664 58.343809 72.173402 56.639209 55.506756 53.075418 47.010637 43.497126 0.000000

O clustermap inclui os resultados do agrupamentos pelo método de Ward, com base nas distâncias acima:

## Perform hierarchical linkage on the distance matrix using Ward's method.
distmat_link = hc.linkage(pwdist, method="ward", optimal_ordering=True )

sns.clustermap(
    distmat,
    annot = True,
    cmap=sns.color_palette("Reds_r"),
    linewidth=1,
    #standard_scale=1,
    row_linkage=distmat_link,
    col_linkage=distmat_link,
    figsize=(8,8)).fig.suptitle('Portuguese Parliament 14th Legislature, Clustermap',y=1)
plt.show()
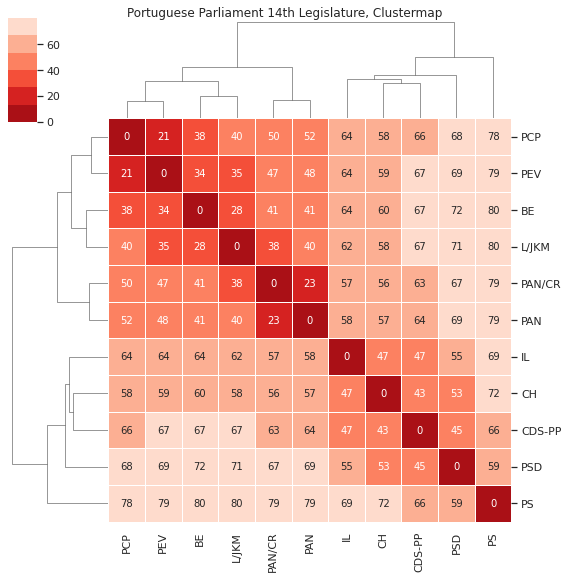
_images/l14_39_0.png

O dendograma respectivo é este, e como se vê é exactamente o mesmo que o apresentado no clustermap

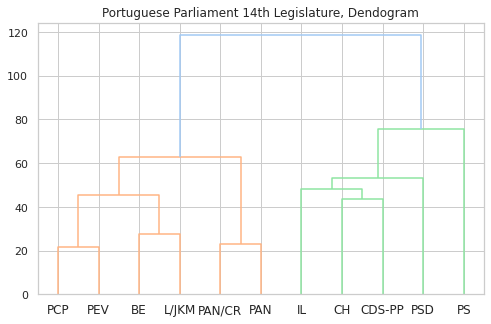
_images/l14_41_0.png

O agrupamento, também derivado do número de partidos, tem diferenças óbvias em relação ao da XIII legislatura: por um lado o posicionamento do PS, por outro a forma como os novos partidos se agrupam (entre si, e com os que já tinham representam).

4.6. Clustering de observações: DBSCAN e Spectrum Scaling

Uma forma diferente de determinar agrupamentos é através de métodos de clustering, que procuram determinar agrupamentos de pontos com base em mecanismos específicos de cada um dos algoritmos.

Vamos demonstrar dois deles, e como passo preliminar vamos transformar a nossa matriz de distâncias: ao contrário do dendograma anterior estes métodos utilizam uma matriz de afinidade, onde valores mais altos significam uma maior semelhança (e, consequentemente, para uma matriz simétrica a diagonal passa de 0 para 1).

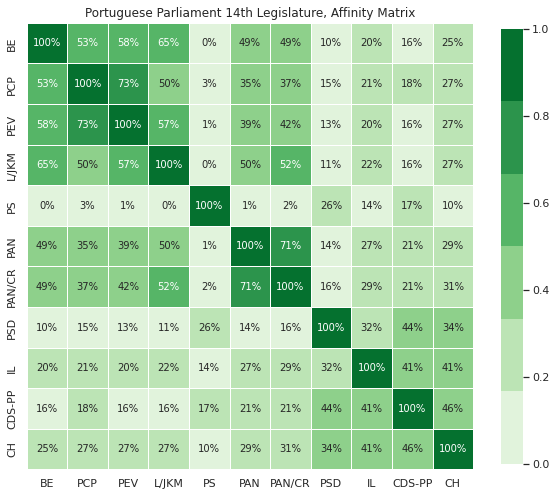
Como passo preliminar normalizamos as distâncias no intervalo [0,1], após o qual obtemos a matriz de afinidade a partir da matriz de distância:

distmat_mm=((distmat-distmat.min().min())/(distmat.max().max()-distmat.min().min()))*1
#pd.DataFrame(distmat_mm, distmat.index, distmat.columns)
affinmat_mm = pd.DataFrame(1-distmat_mm, distmat.index, distmat.columns)
affinmat_mm.style.apply(highlight_diag, axis=None)
  BE PCP PEV L/JKM PS PAN PAN/CR PSD IL CDS-PP CH
BE 1.000000 0.528706 0.578276 0.653852 0.000000 0.493203 0.493357 0.101681 0.197026 0.156553 0.253770
PCP 0.528706 1.000000 0.731467 0.496920 0.026312 0.346525 0.368559 0.153129 0.205250 0.179300 0.273741
PEV 0.578276 0.731467 1.000000 0.567654 0.012989 0.393837 0.416050 0.132238 0.204954 0.158502 0.267629
L/JKM 0.653852 0.496920 0.567654 1.000000 0.001252 0.499101 0.520970 0.106920 0.224172 0.164004 0.270303
PS 0.000000 0.026312 0.012989 0.001252 1.000000 0.013385 0.017118 0.264964 0.141571 0.170861 0.097339
PAN 0.493203 0.346525 0.393837 0.499101 0.013385 1.000000 0.712887 0.141936 0.273526 0.205250 0.291622
PAN/CR 0.493357 0.368559 0.416050 0.520970 0.017118 0.712887 1.000000 0.164378 0.287329 0.211474 0.305786
PSD 0.101681 0.153129 0.132238 0.106920 0.264964 0.141936 0.164378 1.000000 0.316916 0.437192 0.336194
IL 0.197026 0.205250 0.204954 0.224172 0.141571 0.273526 0.287329 0.316916 1.000000 0.407540 0.412045
CDS-PP 0.156553 0.179300 0.158502 0.164004 0.170861 0.205250 0.211474 0.437192 0.407540 1.000000 0.455988
CH 0.253770 0.273741 0.267629 0.270303 0.097339 0.291622 0.305786 0.336194 0.412045 0.455988 1.000000

A matriz de afinidade normalizada pode ser vizualizada de forma semelhante à de distância; como está normalizada e numa escala \( 0 - 1 \) podem-se considerar os valores uma percentagem de afinidade. É importante considerar que, dado o processo de normalização, os valores apresentados ampliam as diferenças.

_images/l14_46_0.png

4.6.1. DBSCAN

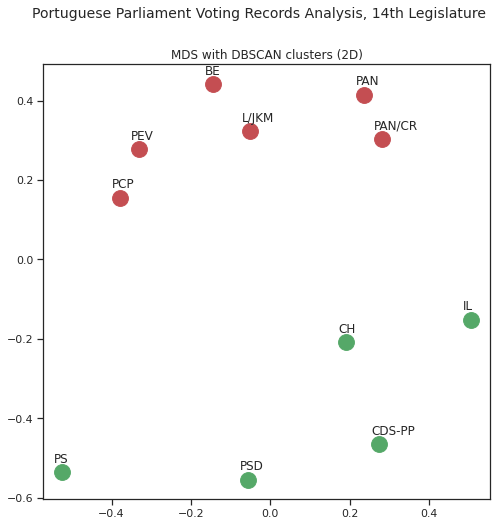
O DBSCAN é algoritmo que, entre outras características, não necessita de ser inicializado com um número pré-determinado de grupos, procedendo à sua identificação através da densidade dos pontos [DBS]: o DBSCAN identifica os grupos de forma automática.

from sklearn.cluster import DBSCAN
dbscan_labels = DBSCAN(eps=0.8).fit(affinmat_mm)
dbscan_labels.labels_
dbscan_dict = dict(zip(distmat_mm,dbscan_labels.labels_))
pd.DataFrame.from_dict(dbscan_dict, orient='index', columns=["Group"]).T
BE PCP PEV L/JKM PS PAN PAN/CR PSD IL CDS-PP CH
Group 0 0 0 0 -1 0 0 -1 -1 -1 -1

Com DBSCAN identificamos 2 grupos, diferentes dos obtidos para a anterior legislatura.

4.6.2. Spectral clustering

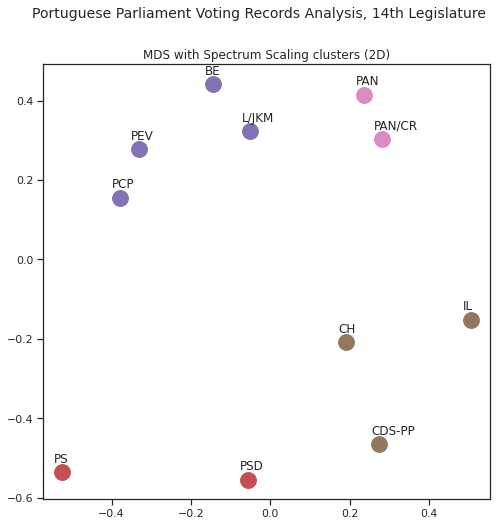
Outra abordagem para efectuar a identificação de grupos passa pela utilização de Spectral Clustering, uma forma de clustering que utiliza os valores-próprios e vectores-próprios de matrizes como forma de determinação dos grupos. Este método necessita que seja determinado a priori o número de clusters; assim, podemos usar este método para agrupamentos mais finos, neste caso identificando 4 grupos (dado o maior número de partidos e deputadas não-inscritas):

from sklearn.cluster import SpectralClustering
sc = SpectralClustering(4, affinity="precomputed",random_state=2020).fit_predict(affinmat_mm)
sc_dict = dict(zip(distmat,sc))

pd.DataFrame.from_dict(sc_dict, orient='index', columns=["Group"]).T
BE PCP PEV L/JKM PS PAN PAN/CR PSD IL CDS-PP CH
Group 1 1 1 1 0 3 3 0 2 2 2

Neste caso, e por determinarmos que devem existir 4 grupos, este algoritmo agrupa PS e PSD, PEV/BE/PCP/JKM, o PAN e Cristina Rodrigues, e o CHEGA, IL e CDS-PP.

Ao MDS pode ser acrescentada informação dos grupos previamente identificados: nestes diagramas usamos as cores para denotar os grupos, tanto para DBSCAN como para Spectral Clustering.

_images/l14_54_0.png
_images/l14_55_0.png

4.6.3. Multidimensional scaling

Não temos ainda uma forma de visualizar a distância relativa de cada partido em relação aos outros com base nas distâncias/semelhanças: temos algo próximo com base no dendograma mas existem outras formas de visualização interessantes.

Uma das formas é o multidimensional scaling que permite visualizar a distância ao projectar em 2 ou 3 dimensões (também conhecidas como dimensões visualizavies) conjuntos multidimensionais, mantendo a distância relativa [ZWH15].

from sklearn.manifold import MDS


## Graphic options
sns.set()
sns.set_style("whitegrid")

fig, ax = plt.subplots(figsize=(8,8))

plt.title('Portuguese Parliament Voting Records Analysis, 14th Legislature', fontsize=14)

for label, x, y in zip(distmat_mm.columns, coords[:, 0], coords[:, 1]):
    ax.scatter(x, y, s=250)
    ax.axis('equal')
    ax.annotate(label,xy = (x-0.02, y+0.025))
plt.show()
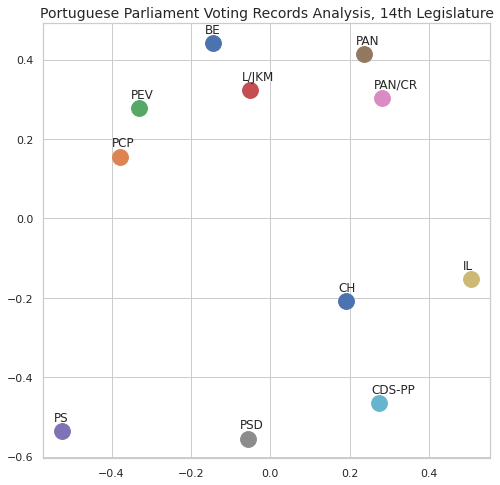
_images/l14_58_0.png

Por último, o mesmo MDS em 3D, e em forma interactiva:

mds = MDS(n_components=3, dissimilarity='precomputed',random_state=1234, n_init=100, max_iter=1000)
results = mds.fit(distmat.values)
parties = distmat.columns
coords = results.embedding_
import plotly.graph_objects as go
# Create figure
fig = go.Figure()

# Loop df columns and plot columns to the figure
for label, x, y, z in zip(parties, coords[:, 0], coords[:, 1], coords[:, 2]):
    fig.add_trace(go.Scatter3d(x=[x], y=[y], z=[z],
                        text=label,
                        textposition="top center",
                        mode='markers+text', # 'lines' or 'markers'
                        name=label))
fig.update_layout(
    width = 1000,
    height = 1000,
    title = "14th Legislature: 3D MDS",
    template="plotly_white",
    showlegend=False
)
fig.update_yaxes(
    scaleanchor = "x",
    scaleratio = 1,
  )
plot(fig, filename = 'l14-3d-mds.html')
display(HTML('l14-3d-mds.html'))