7. Suporte, distâncias e aprovações na linha temporal¶

There is little danger that any student, however idle or stupid, will fail to get some result; but there is great danger that he will be led astray, obsessed and overwhelmed by his results, even though it be by those which it is necessary that he should attain. Too often, moreover, he mistaketh the first resting-place for the goal, and taketh off his armour as if he were a victor ere the fight is well begun.

—Aleister Crowley, «Liber O vel Manus et Sagittæ, sub figura VI»

7.1. Proximidades e distância ao longo do tempo¶

As análises feitas até à data têm focado a proximidade e distância - em várias dimensões diferentes - dos vários partidos, e se é verdade que a utilização das visualizações originais (clustermaps, MDSs, dendogramas, etc) é feita de forma a permitir a comparação de vários anos e legislatura, isso é conseguido através da comparação dos gráficos que representam a situação em determinado momento.

Um pedido comum é visualizar como evoluem as proximidades/aprovações/distâncias ao longo do tempo, de uma forma que coloque a dimensão temporal em primeiro plano: esta actualização adiciona novas formas de apresentar os dados que vão nesse sentido.

Uma das vantagens dos clustermaps e gráficos em 2D com a posição relativa dos partidos é a forma como, de forma muito imediata, permitem uma leitura dos dados através de uma única imagem: um único clustermap permite identificar a proximidade e de que forma se agrupam os partidos para todo o período em análise. Ao promover a dimensão temporal torna-se difícil condensar os dados desta forma, pois mostrar todas as distâncias entre todos os partidos numa linha do tempo seria de tal forma confuso ao ponto de ser incompreensível. Optámos por separar os partidos (de forma semelhante ao que já foi feito para apresentar dados relativos às aprovações de propostas) e mostrar uma linha temporal como eixo principal.

Estes dados são complementares aos já existentes: pode-se imaginar que a posição de todos os partidos em determinada altura, tal como apresentada nesta actualização de forma separada, corresponde ao clustermap e gráfico de distância 2D correspondente.

7.2. Âmbito e pressupostos¶

Optámos por incluir os dados da XIV e XV legislatura (até à data), de forma a permitir uma leitura que inclua mais anos e permita, eventualmente, uma análise mais aprofundada. Esta opção acarreta alguns compromissos, o mais importante o de apenas incluir os partidos que estão presentes em ambas as legislaturas. Isto exclui o CDS-PP e o PEV.

No caso dos deputados únicos, os votos do Livre incluem os da deputada Joacine Kata Moreira.

São contabilizados apenas os votos

Total de votações: 1905

Data limite inferior: 2019-11-15

Data limite superior: 2023-04-28

7.3. Apoios a propostas¶

Começamos pela análise que leva em conta os autores das propostas, em moldes semelhantes à análise já feita, mas focando na evolução ao longo do tempo para cada partido.

Como neste caso sabemos o autor da proposta, podemos utilizar uma valorização dos votos que assenta não na distância, mas na posição em relação à proposta:

A Favor: +1
Contra: -1
Abstenção/Ausência: 0

Ao irmos somando os votos ao longo do tempo, a cada momento o valor de “suporte” representa o acumulado de todos os votos até à data, indo subindo ou descendo conforme os padrões de votação.

Intuitivamente podemos imagine os seguintes cenários:

Um partido que apoie sempre as propostas de outro irá ter uma recta em sentido ascendente, pois a cada votação o valor acumulado é +1 que o anterior.
Um partido que vote sempre contra as propostas de outro irá ter uma recta em sentido descendente, pois a cada votaçãi o valor acumulado é -1 que o anterior.
Um partido que se abstenha sempre das propostas de outro ir«a ter uma recta horizontal, pois o valor irá permanecer em 0 desde a origem.

Mais genericamente, em termos de tendências:

Rectas sem grandes oscilações em termos de direcção indicam, tendencialmente, um comportamento uniforme ao longo do tempo.
Zigue-zagues e outras oscilações de direcção indicam uma variação de comportamento ao longo do tempo.

O eixo horizontal representa as datas das votações, e o vertical o valor acumulado conforme a quantificação descrita acima.

sns.set_style("whitegrid")

parties = ['BE', 'PCP', 'L','PS', 'PAN','PSD','IL','CH' ]
gpsubs = submissions_ini_hm
for party in parties:
    subp = gpsubs[gpsubs['GP'] == party]
    subp = subp[parties]
    #fig = plt.figure()
    subp = subp.drop(party, axis=1)
    ax = subp.resample("1M").sum().cumsum().plot(kind="line", title=party, figsize=(15,5))
    
    for line, name in zip(ax.lines, subp.columns):
        y = line.get_ydata()[-1]
        ax.annotate(line.get_label(), xy=(1,y), xytext=(6,0), color=line.get_color(), 
            xycoords = ax.get_yaxis_transform(), textcoords="offset points",
            size=10, va="center")

    #plt.legend(loc='lower left')
    plt.axvline(pd.to_datetime('2021-11-26'), color='grey', linestyle='--', lw=1)
    plt.axvline(pd.to_datetime('2022-03-29'), color='grey', linestyle='--', lw=1)
    ax.text(pd.to_datetime('2022-03-29'), 0.99, 'XV', color='grey', ha='right', va='top', rotation=90,
            transform=ax.get_xaxis_transform())
    ax.text(pd.to_datetime('2021-11-26'), 0.99, 'XIV', color='grey', ha='right', va='top', rotation=90,
            transform=ax.get_xaxis_transform())
    ax.get_legend().remove()
    plt.tight_layout()

    #plt.show()

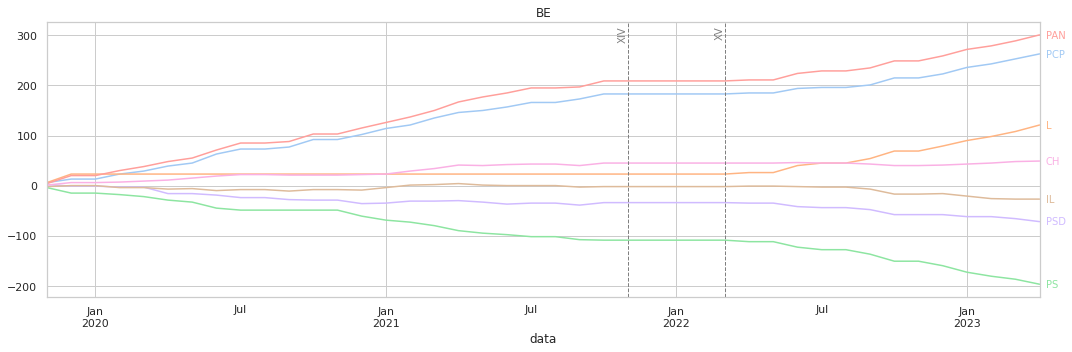
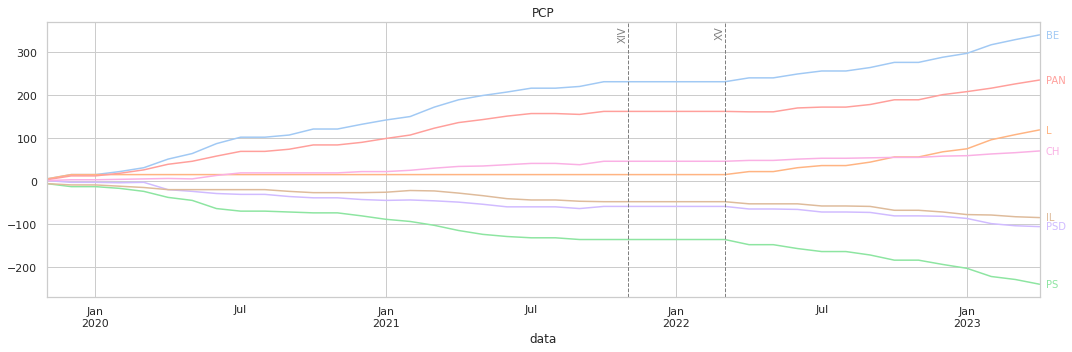
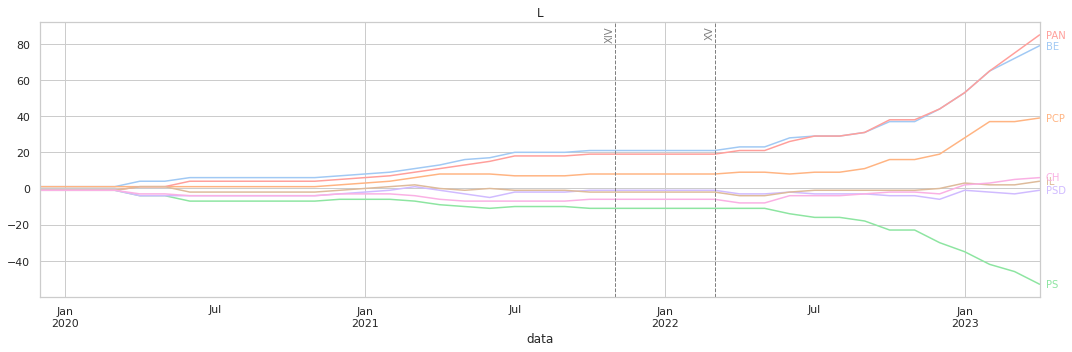
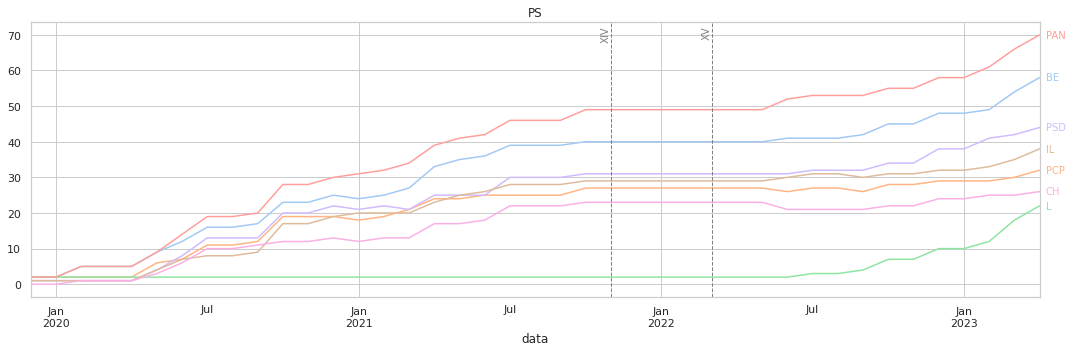
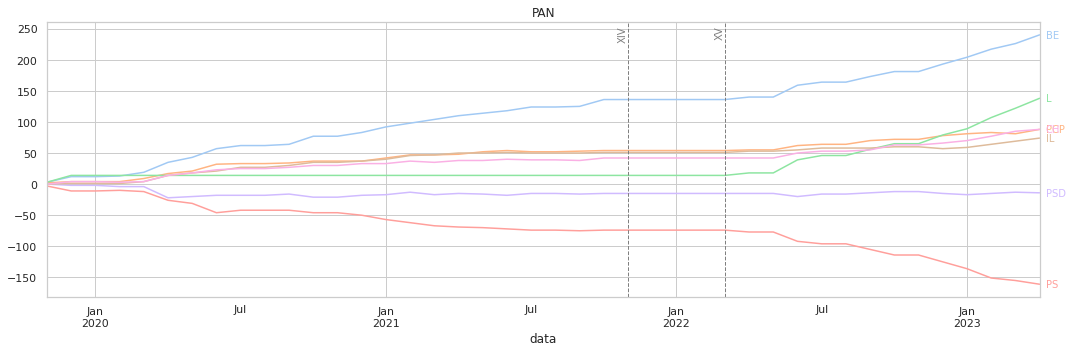
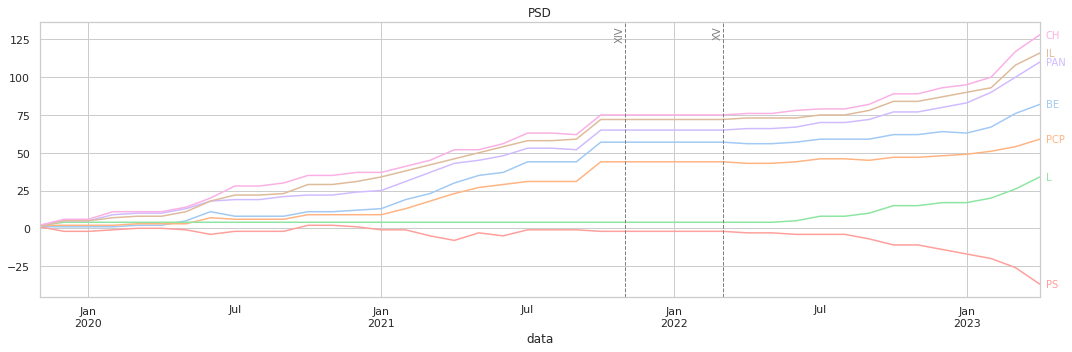
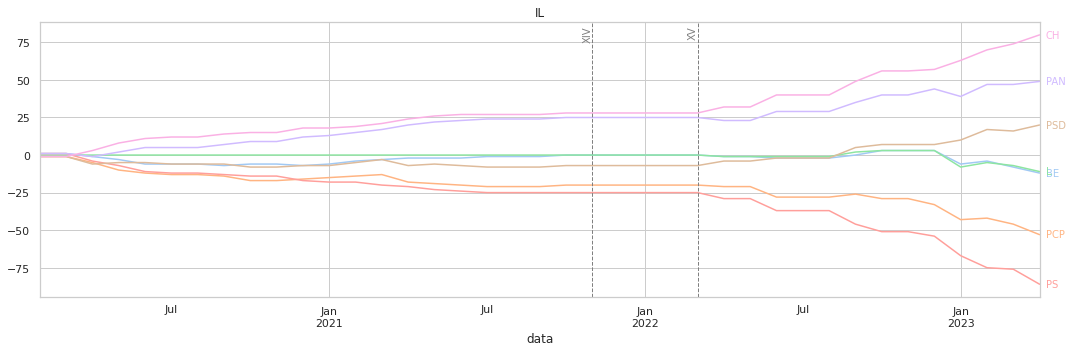
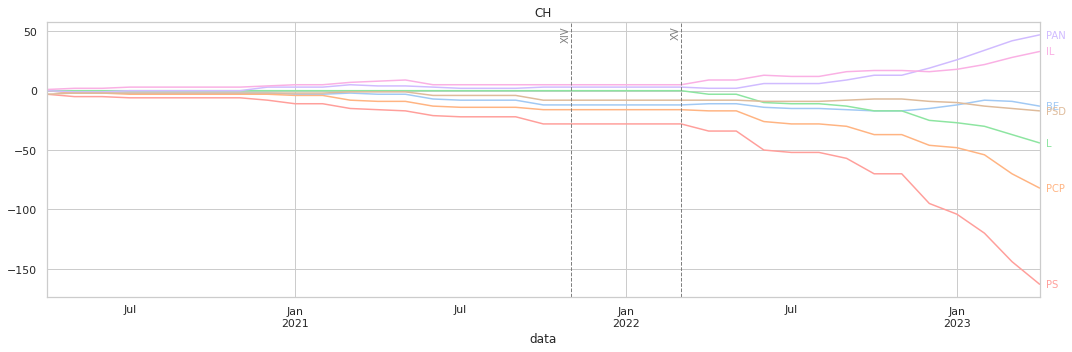
A maior parte dos gráficos mostra-nos uma tendência constante de votações, sem grandes variações abruptas. Os resultados finais têm, de uma forma imediata, relação com os clustermaps anterire

7.4. Distância ao longo do tempo¶

Medir a distância é diferente de medir o apoio a propostas; relembrando:

As distâncias são obtidas pela concordância ou diferença no sentido de voto entre os pares de partidos, independentemente da origem da matéria em votação.
São analisadas todas as votações, sendo o universo maior que a análisr anterior (que contempla apenas as votações na generalidade).

Se na análise anterior podiamos usar 1/0/-1 para medir o grau de apoio, na distância o que medimos é a diferença entre posições ao longo do tempo:

Se dois partidos votam da mesma forma, a distância é 0.
Se dois partidos votam de forma diferente, mas não diametralmente oposta, a distância é 1 (por exemplo, se um partido vota contra e o outro se abstem).
Se dois partidos votam de forma diametralmente oposta, a distância é 2 (por exemplo, um vota contra e outra vota a favor).

Esta é exactamente a mesma abordagem usada para as análises anterior, para as quais remetemos para detalhes adicionais.

Ao medirmos a distância, o gráfico irá ter uma forma diferente: aqui, um partido que vote sempre da mesma forma que o partido em análise irá ter uma linha horizontal, por a distância será sempre 0. Não existem valores negativos, pois a distância mínima entre dois partidos é 0: quanto mais “cresce” a linha mais distante o partido está.

Acrescentámos duas linhas verticais que marcam o fim da XIV legislatura, e o início da XV, para de forma mais clara se poder observar eventuais mudanças na dinâmica das votações.

distances = {}

for party in all_parties:
    party_dist_df = all_ts
    party_dist_df = party_dist_df
    for dist_party in all_parties:
        party_dist_df[str("dist_" + dist_party)] = abs(party_dist_df[party]-party_dist_df[dist_party])
    distances[party] = party_dist_df.copy(deep=True)
    party_dist_df = party_dist_df.drop(str("dist_" + party), axis=1)

    #fig = plt.figure()
    ax = party_dist_df.filter(regex=("dist_.*")).resample("1W").sum().cumsum().plot(kind="line", title=party, figsize=(15,8))
    #ax = party_dist_df.filter(regex=("dist_.*")).cumsum().plot(kind="line", title=party, figsize=(15,8))
    
    for line, name in zip(ax.lines, party_dist_df.columns):
        y = line.get_ydata()[-1]
        ax.annotate(line.get_label().replace("dist_",""), xy=(1,y), xytext=(6,0), color=line.get_color(), 
                xycoords = ax.get_yaxis_transform(), textcoords="offset points",
                size=10, va="center")
    #plt.legend(loc='upper left'
    ax.get_legend().remove()
    plt.axvline(pd.to_datetime('2021-11-26'), color='grey', linestyle='--', lw=1)
    plt.axvline(pd.to_datetime('2022-03-29'), color='grey', linestyle='--', lw=1)
    ax.text(pd.to_datetime('2022-03-29'), 0.99, 'XV', color='grey', ha='right', va='top', rotation=90,
            transform=ax.get_xaxis_transform())
    ax.text(pd.to_datetime('2021-11-26'), 0.99, 'XIV', color='grey', ha='right', va='top', rotation=90,
            transform=ax.get_xaxis_transform())
    plt.tight_layout()

    #plt.show()
    #display(party_dist_df)

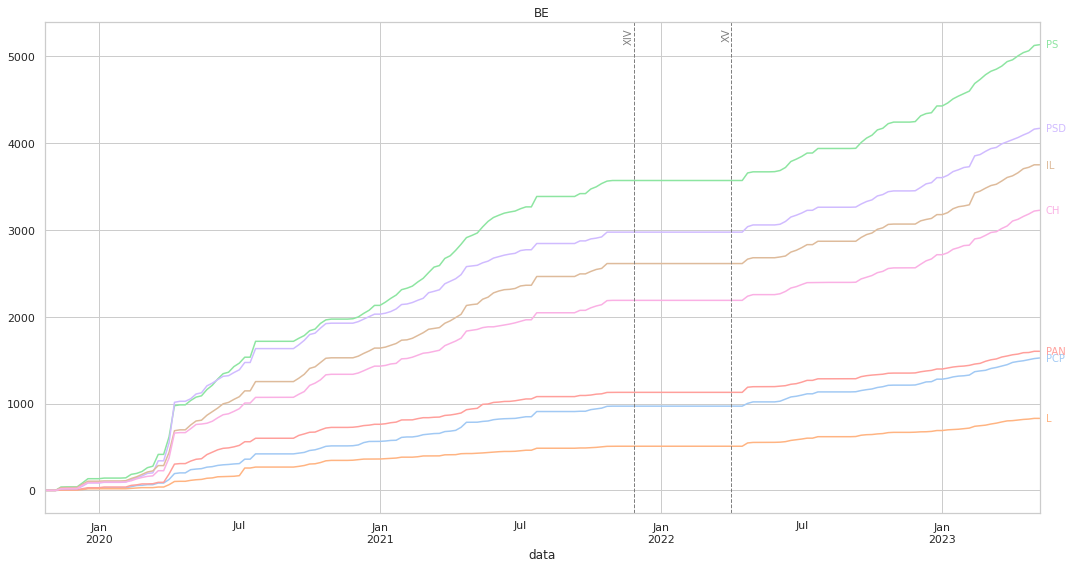
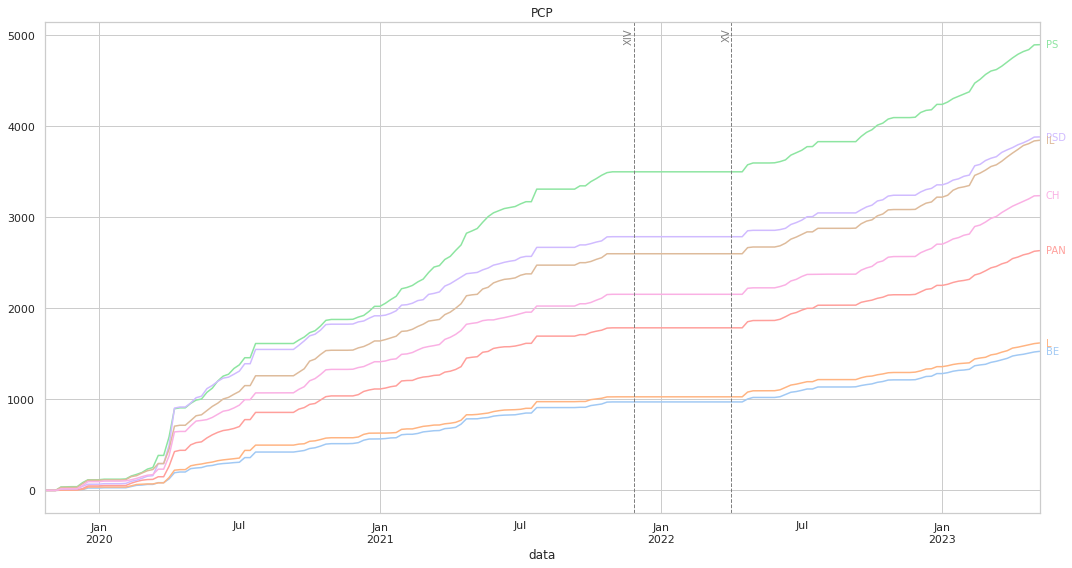
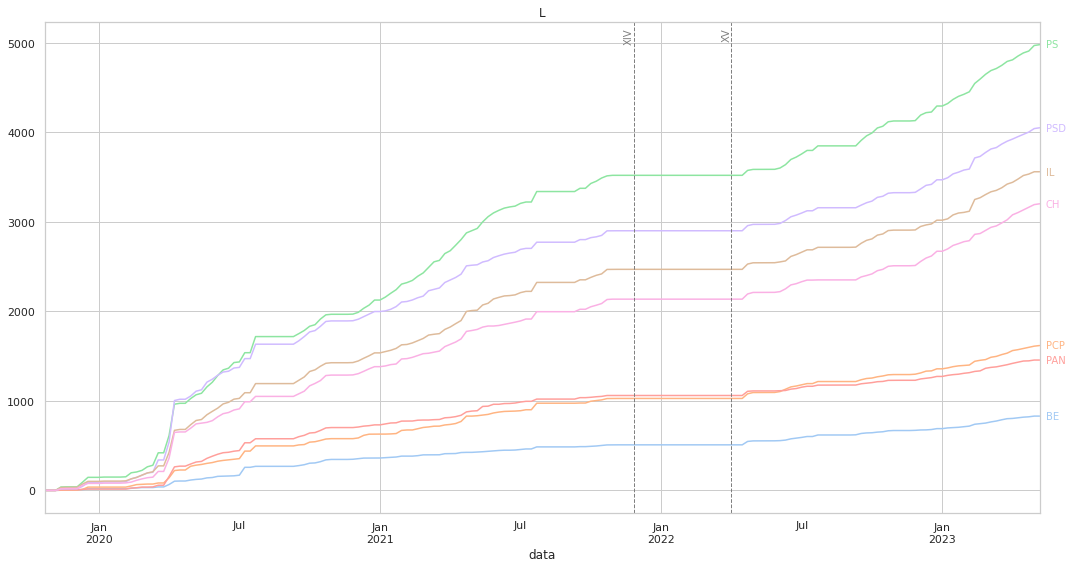
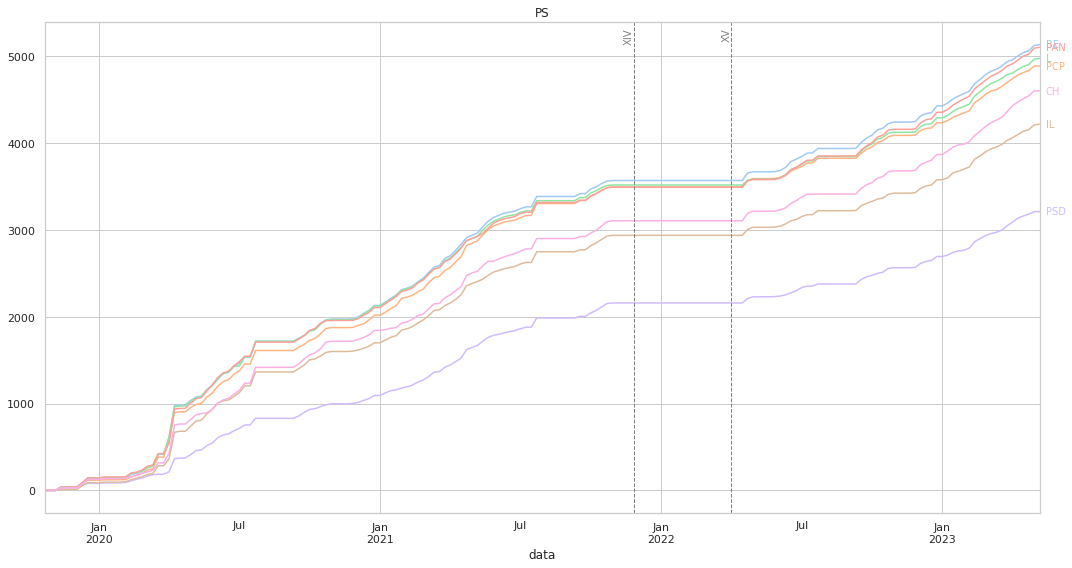
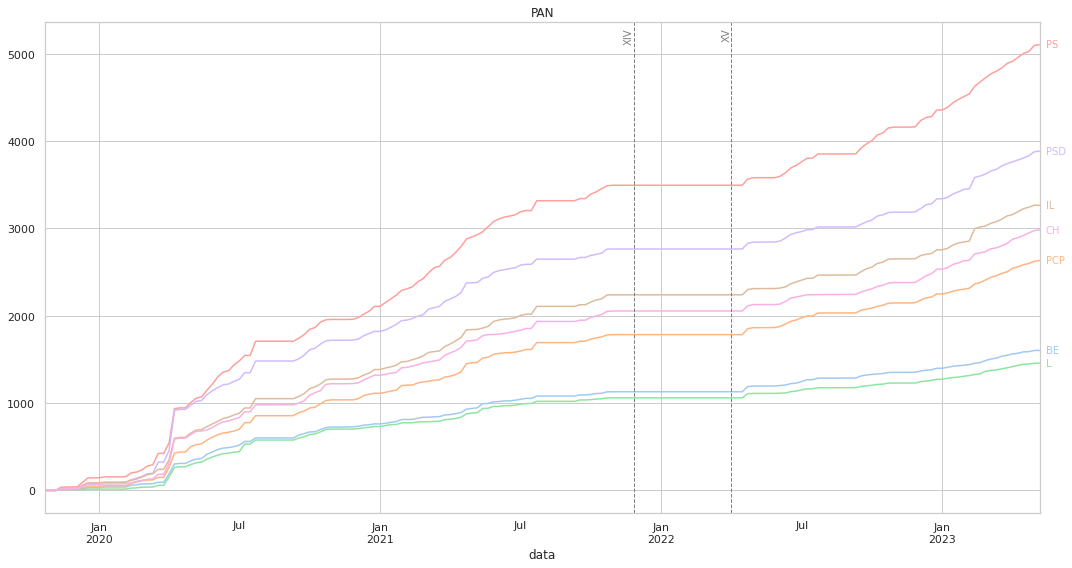
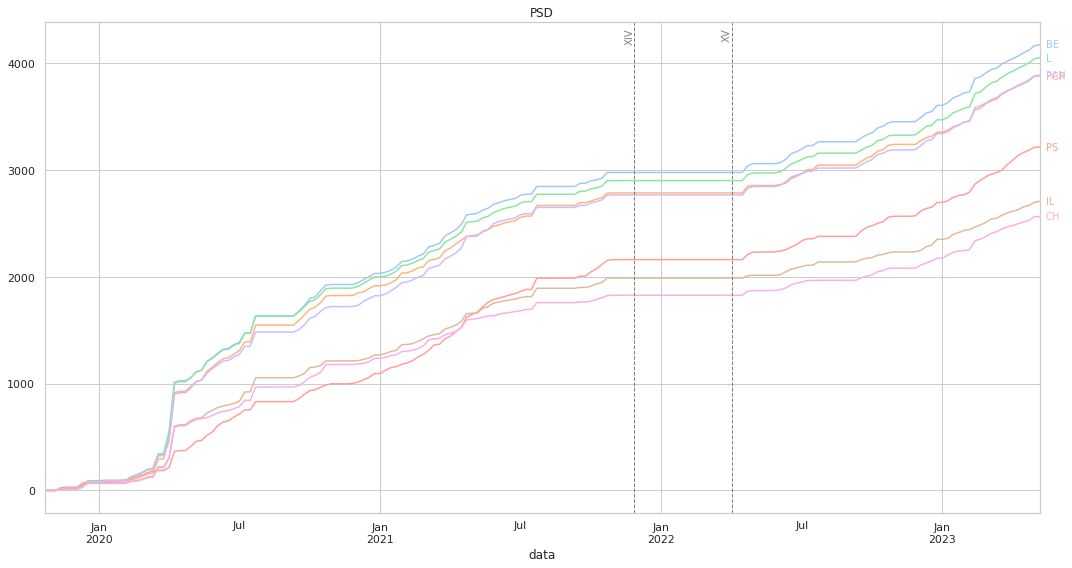
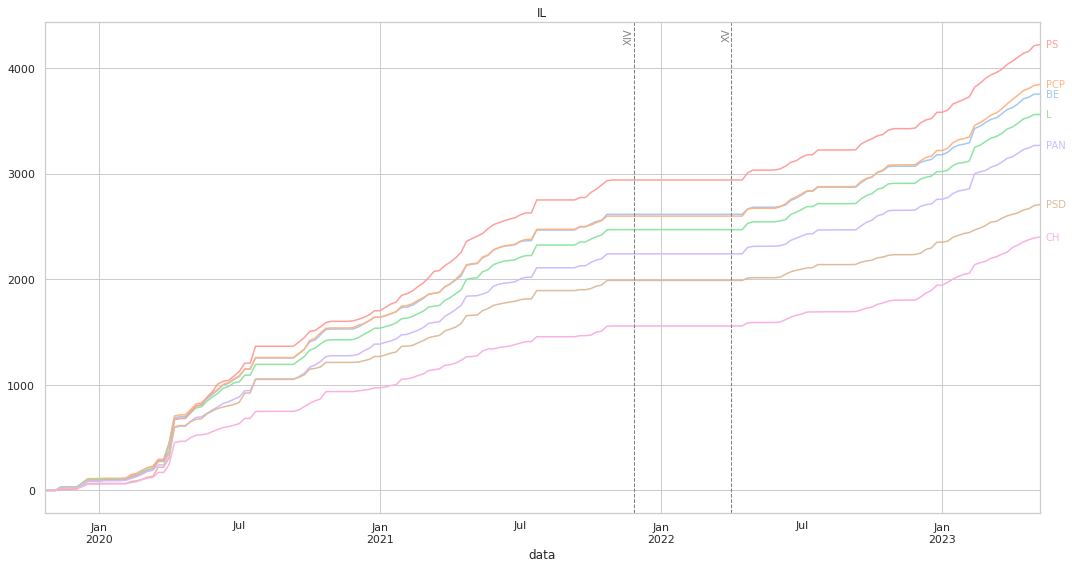
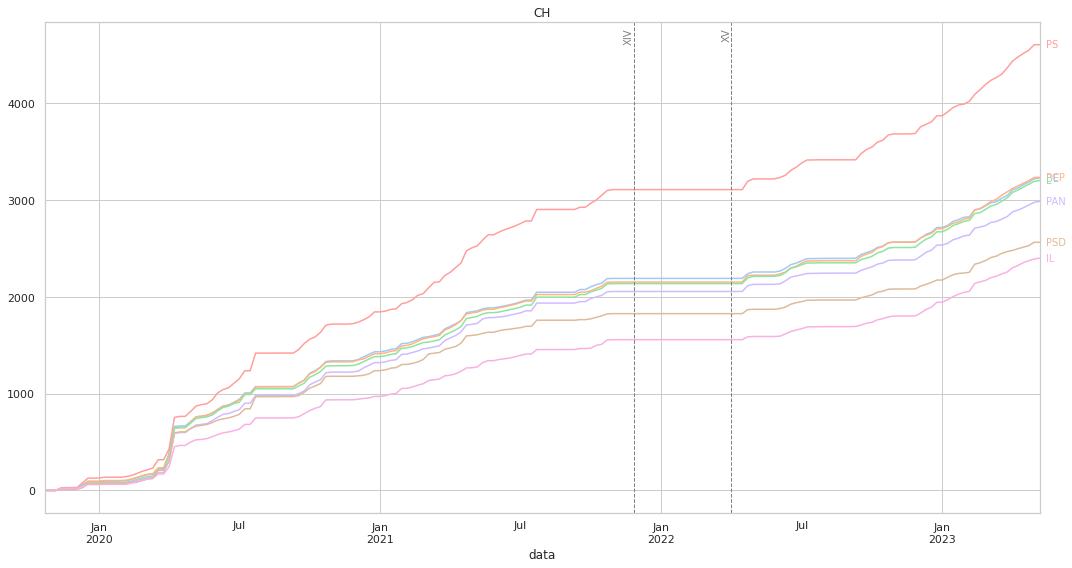
Mais uma vez, os valores “finais” estão alinhados com o que pode ser visto nos clustermaps.

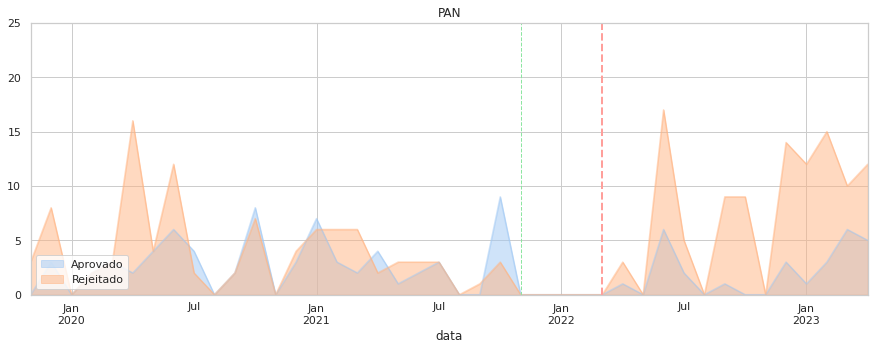
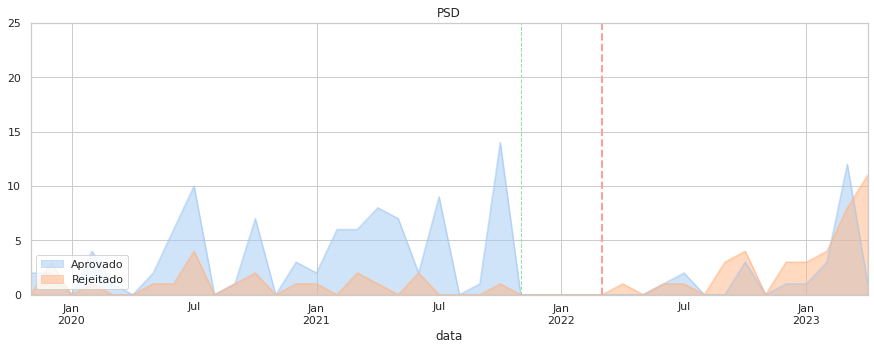
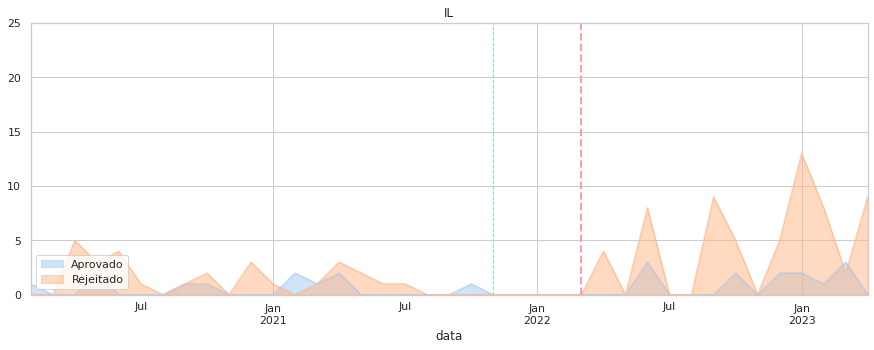
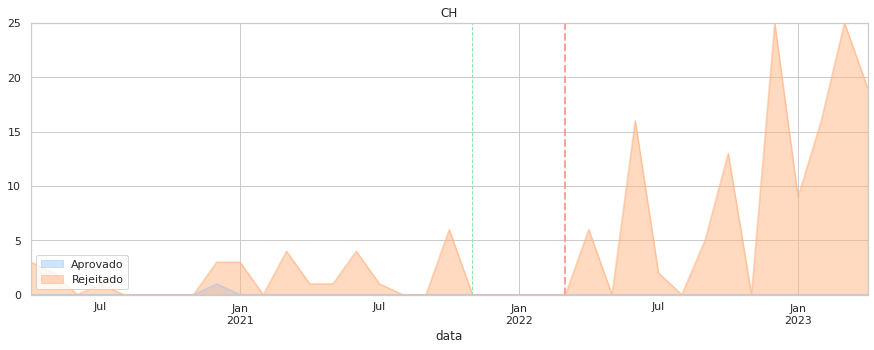
7.5. Aprovações¶

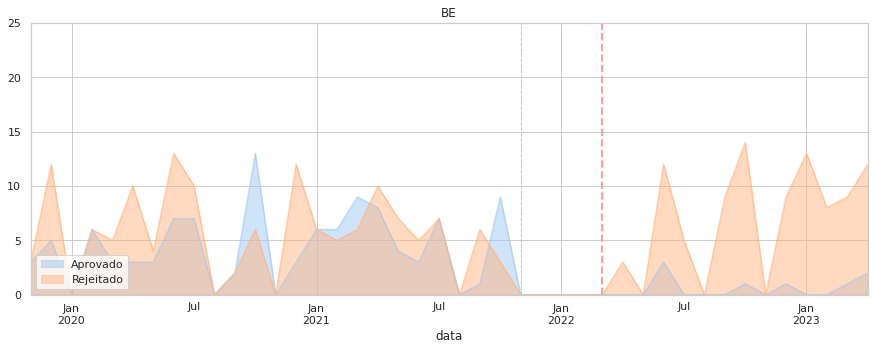
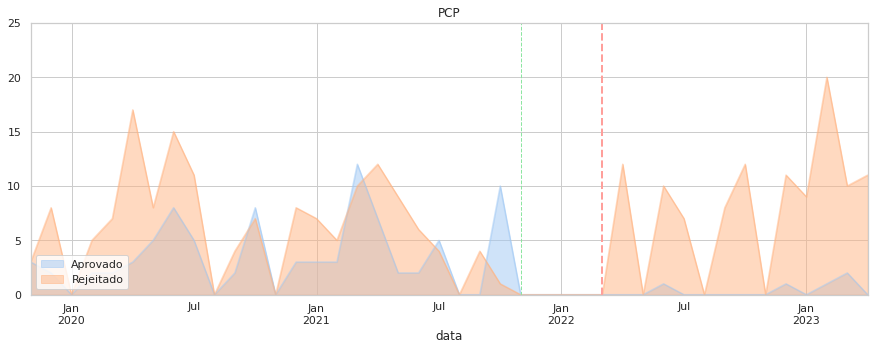
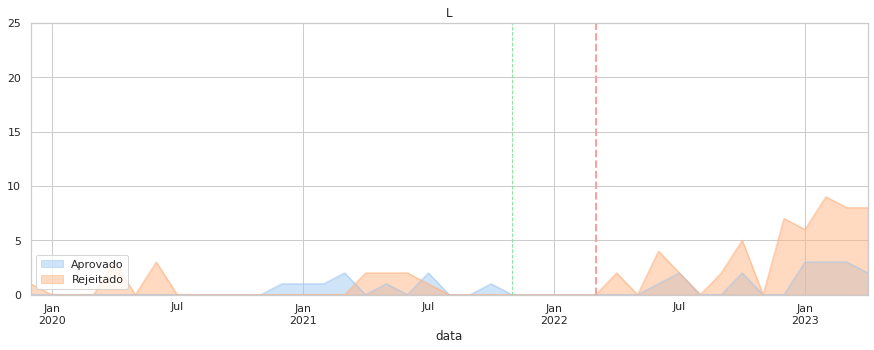
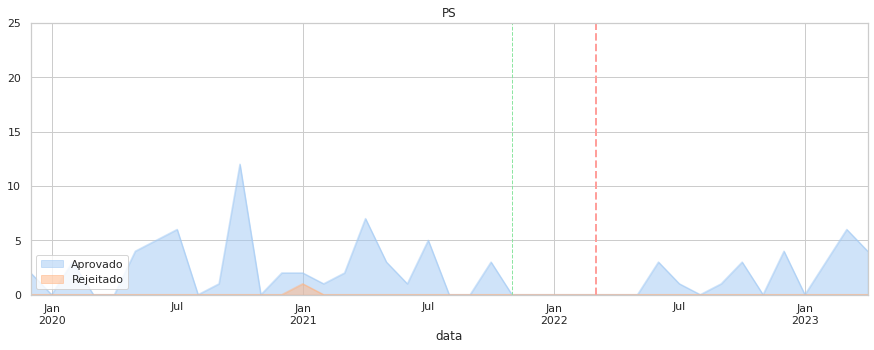
Por último, foquemos as taxas de aprovação ao longo do tempo. Aqui o que é medido é o sucesso das propostas de cada partido, o que depende do apoio parlamentar que tenham.

Note-se que a quantidade de propostas de cada partido pode ser substancialmente diferente (valor indicado no eixo vertical).

parties = ['BE', 'PCP', 'L', 'PS', 'PAN','PSD','IL','CH' ]
gpsubs= submissions_ini_hm.copy(deep=True)

#gpsubs = submissions_ini_hm
for party in parties:
    subp = gpsubs[gpsubs['GP'] == party]
    result_dummies = pd.get_dummies(subp["resultado"])
    result_dummies.columns = ['Aprovado','Rejeitado']
    subp = pd.concat([subp, result_dummies], axis=1)
    subp = subp[["Aprovado", "Rejeitado"]]
    ax = subp.resample("1M").sum().plot(kind="area", stacked=False, title=party, figsize=(15,5))
    ax.set_ylim([0, 25])
    plt.legend(loc='lower left')
    plt.axvline(pd.to_datetime('2021-11-26'), color='g', linestyle='--', lw=1)
    plt.axvline(pd.to_datetime('2022-03-29'), color='r', linestyle='--', lw=2)
    plt.show()
    #display(subp.resample("1M").sum().cumsum())